
分析 利用两点间距离公式及配方法能求出A,B两点间的距离的最小值.
解答 解:∵A(1-t,1-t,t),B(2,t,t),
∴|AB|=$\sqrt{(1-t-2)^{2}+(1-t-t)^{2}+(t-t)^{2}}$
=$\sqrt{(-1-t)^{2}+(1-2t)^{2}}$
=$\sqrt{5{t}^{2}-2t+2}$
=$\sqrt{5(t-\frac{1}{5})^{2}+\frac{9}{5}}$,
∴当t=$\frac{1}{5}$时,
A,B两点间的距离取最小值|AB|min=$\sqrt{\frac{9}{5}}=\frac{3\sqrt{5}}{5}$.
故答案为:$\frac{3\sqrt{5}}{5}$.
点评 本题考查两点间距离的最小值的求法,是基础题,解题时要认真审题,注意两点意距离公式的合理运用.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
中秋节吃月饼是我国的传统习俗,设一盘中盛有7块月饼,其中五仁月饼2块,莲蓉月饼3块,豆沙月饼2块,这三种月饼的形状大小完全相同,从中任取3块.
(Ⅰ)求这三种月饼各取到1块的概率;
(Ⅱ)设 表示取到的豆沙月饼的个数,求
表示取到的豆沙月饼的个数,求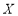 的分布列,数学期望与方差.
的分布列,数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com