练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．（x2+$\frac{1}{{x}^{2}}$-2）3展开式中的常数项为-20．

    分析 由于（x2+$\frac{1}{{x}^{2}}$-2）3=${（x-\frac{1}{x}）}^{6}$，在它的二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．

    解答 解：∵（x2+$\frac{1}{{x}^{2}}$-2）3=${（x-\frac{1}{x}）}^{6}$ 的展开式的通项公式为 Tr+1=${C}_{6}^{r}$•（-1）r•x6-2r，
    令6-2r=0，可得r=3，故展开式中的常数项为-${C}_{6}^{3}$=-20，
    故答案为：-20．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届河北沧州市高三9月联考数学（文）试卷（解析版） 题型：解答题

    为了弘扬民族文化，某校举行了“我爱国学，传诵经典”考试，并从中随机抽取了100名考生的成绩（得分均为整数，满分100分）进行统计制表，其中成绩不低于80分的考生被评为优秀生，请根据频率分布表中所提供的数据，用频率估计概率，回答下列问题．

    分组

    频数

    频率

    5

    35

    25

    15

    合计

    100

    （Ⅰ）求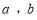的值及随机抽取一考生恰为优秀生的概率；

    （Ⅱ）按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动，求其中优秀生的人数；

    （Ⅲ）在第（Ⅱ）问抽取的优秀生中指派2名学生担任负责人，求至少一人的成绩在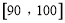的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．正三角形ABC的边长为4，P、Q分别是AB、AC上的点，PQ∥BC，将△ABC沿PQ折起，使平面APQ⊥平面BPQC，设折叠后A、B两点间的距离为d，则d的最小值为（　　）
    A．10B．$2\sqrt{5}$C．$2\sqrt{10}$D．$\sqrt{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．对于定义在数集R上的函数f（x），如果存在实数x0，使f（x0）=x0，则x0叫作函数f（x）的一个不动点．已知f（x）=x2+2ax+1不存在不动点，那么a的取值范围是$（-\frac{1}{2}，\frac{3}{2}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．以C（4，-6）为圆心，半径等于3的圆的方程为（x-4）2+（y+6）2=9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知角α的终边和单位圆的交点为P（$\frac{3}{5}$，$\frac{4}{5}$），则sinα+2cosα的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知数列{an}满足${a_1}=1，\frac{{n{a_n}-2{a_{n+1}}}}{{{a_{n+1}}}}=n，n∈{N^*}$，则数列{an}的通项公式是an=$\frac{2}{n（n+1）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知A（1-t，1-t，t），B（2，t，t），则A，B两点间的距离的最小值是$\frac{3\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若直线x+y=1与曲线y=$\sqrt{a-{x^2}}$（a＞0）恰有一个公共点，则a的取值范围是（　　）
    A．$\frac{1}{2}$＜a＜1B．$\frac{1}{2}$≤a＜1C．a＞1或$a=\frac{1}{2}$D．$a=\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案