
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:
将长度为 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时 的最大值为4.则:
的最大值为4.则:
(1)当 时,
时, 的最大值为________;(2)当
的最大值为________;(2)当 时,
时, 的最大值为________.
的最大值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线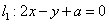 ,
, ,和圆:
,和圆: 相切,则实数
相切,则实数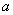 的取值范围是( )
的取值范围是( )
A.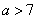 或
或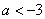 B.
B.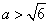 或
或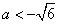
C.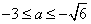 或
或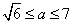 D.
D.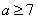 或
或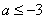
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)= +cos2x-sin2x.
+cos2x-sin2x.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)在所给坐标系中画出函数在区间[ π,
π, π]的图像(只作图不写过程).
π]的图像(只作图不写过程).

查看答案和解析>>
科目:高中数学 来源: 题型:
设直线l1的参数方程为 (t为参数),以坐标原点为极点,x轴非负半轴为极轴建立极坐标系,另一直线l2的方程为ρsin θ-3ρcos θ+4=0,若直线l1与l2间的距离为
(t为参数),以坐标原点为极点,x轴非负半轴为极轴建立极坐标系,另一直线l2的方程为ρsin θ-3ρcos θ+4=0,若直线l1与l2间的距离为 ,则实数a的值为________.
,则实数a的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com