
【题目】已知抛物线![]() ,过其焦点
,过其焦点![]() 作两条相互垂直且不平行于坐标轴的直线,它们分别交抛物线
作两条相互垂直且不平行于坐标轴的直线,它们分别交抛物线![]() 于点
于点![]() 、
、![]() 和点
和点![]() 、
、![]() ,线段
,线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)求![]() 面积的最小值;
面积的最小值;
(Ⅲ)过![]() 、
、![]() 的直线
的直线![]() 是否过定点?若是,求出定点坐标,若不是,请说明理由.
是否过定点?若是,求出定点坐标,若不是,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)4;(Ⅲ)直线
;(Ⅱ)4;(Ⅲ)直线![]() 恒过定点
恒过定点![]() .
.
【解析】
试题分析:(Ⅰ)要求轨迹方程,而且抛物线的弦中点轨迹方程,可设中点![]() ,弦两端点为
,弦两端点为![]() ,
,![]() ,由点差法得直线斜率
,由点差法得直线斜率![]() ,又此斜率为
,又此斜率为![]() ,两者相等可得轨迹方程;为了(Ⅱ)的需要,设
,两者相等可得轨迹方程;为了(Ⅱ)的需要,设![]() 方程为
方程为![]() ,代入抛物线方程后可得
,代入抛物线方程后可得![]() 的一元二次方程,从而有
的一元二次方程,从而有![]() ,那么有
,那么有![]() ,即把
,即把![]() 用
用![]() 表示,同样把
表示,同样把![]() 也用
也用![]() 表示,后消去
表示,后消去![]() 可得轨迹方程;(Ⅱ)在(Ⅰ)的基础上,得
可得轨迹方程;(Ⅱ)在(Ⅰ)的基础上,得![]() 坐标,可求得
坐标,可求得![]() ,把其中的
,把其中的![]() 用
用![]() 代替,可得得
代替,可得得![]() 坐标,
坐标,![]() ,由
,由![]() 得
得![]() 的函数,可得最小值;(Ⅲ)利用(Ⅱ)中
的函数,可得最小值;(Ⅲ)利用(Ⅱ)中![]() 的坐标求出直线
的坐标求出直线![]() 的方程(与
的方程(与![]() 有关),变形后发现其过定点,同时证明
有关),变形后发现其过定点,同时证明![]() 斜率不存在时也过这个定点.
斜率不存在时也过这个定点.
试题解析:(Ⅰ)由题设条件得焦点坐标为![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,![]() .
.
联立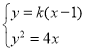 ,得
,得![]() .
.
![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,∴
,∴![]() .
.
∴线段![]() 的中点
的中点![]() 的轨迹方程为:
的轨迹方程为:![]() .
.
(Ⅱ)由(Ⅰ)知: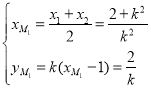 .
.
同理,设![]() ,则
,则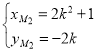 .
.
∴![]() ,
,
![]() ,
,
因此![]() .
.
当且仅当![]() ,即
,即![]() 时,
时,![]() 取到最小值4.
取到最小值4.
(Ⅲ)当![]() 时,由(Ⅱ)知直线
时,由(Ⅱ)知直线![]() 的斜率为:
的斜率为:![]() ,
,
所以直线![]() 的方程为:
的方程为: ![]() ,即
,即![]() ,(*)
,(*)
当![]() ,
,![]() 时方程(*)对任意的
时方程(*)对任意的![]() 均成立,即直线
均成立,即直线![]() 过点
过点![]() .
.
当![]() 时,直线
时,直线![]() 的方程为:
的方程为:![]() ,也过点
,也过点![]() .
.
所以直线![]() 恒过定点
恒过定点![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某小型餐馆一天中要购买![]() ,
,![]() 两种蔬菜,
两种蔬菜,![]() ,
,![]() 蔬菜每公斤的单价分别为2元和3元.根据需要
蔬菜每公斤的单价分别为2元和3元.根据需要![]() 蔬菜至少要买6公斤,
蔬菜至少要买6公斤,![]() 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,![]() ,
,![]() 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 轴交点为
轴交点为![]() ,与
,与![]() 的交点为
的交点为![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的垂直平分线
的垂直平分线![]() 与
与![]() 相交于
相交于![]() 两点,且
两点,且![]() 四点在同一圆上,求
四点在同一圆上,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=ax2+bx+c(a≠0)是偶函数,则g(x)=ax3+bx2+cx是( )
A.奇函数 B.偶函数 C.非奇非偶函数 D.既奇又偶函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com