练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．F1、F2是椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的两焦点，AB是过F2的弦，则△ABF1的周长为20．

    分析 根据椭圆的方程算出a=5，由椭圆的定义得到|AF1|+|AF2|=|BF1|+|BF2|=2a=10，由此将△ABF1的周长分成|AF1|+|AF2|、|BF1|+|BF2|两部分，即可得到所求△ABF1的周长

    解答 解：∵椭圆的方程为$\frac{x^2}{25}$+$\frac{y^2}{16}$=1，
    ∴a=5，
    根据椭圆的定义，得|AF1|+|AF2|=|BF1|+|BF2|=2a=10，
    ∴△ABF1的周长|AF1|+|BF1|+|AB|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=20，
    故答案为：20．

    点评 本题给出椭圆经过右焦点的弦AB与左焦点F1构成的三角形，求△ABF1的周长．着重考查了椭圆的定义与标准方程的知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆c1：$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1的左、右焦点分别为F1，F2，过点F1作垂直于x轴的直线l1，直线l2垂直l1于点P，线段PF2的垂直平分线交l2于点M
    （1）求点M的轨迹C2的方程
    （2）过点F2作两条互相垂直的直线AC，BD，且分别交椭圆于A，B，C，D，求四边形ABCD面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设0≤x≤2，则函数f（x）=$\frac{1}{2}$×4x-3•2x+5的最大值是$\frac{5}{2}$，最小值是$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．设x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥x\\ 4x+3y≤12\end{array}\right.$，则$\frac{2y-x+1}{x+1}$的最大值是9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知cosαcosβ=cosα+cosβ+3，则sin（α+β）=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在锐角三角形ABC中，a，b，c是角A，B，C的对边，已知（b2+c2-a2）tanA=$\sqrt{3}$bc
    （1）求角A的大小，
    （2）若f（B）=sinBcosB-$\sqrt{3}{cos^2}B+\sqrt{3}$，求f（B）范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

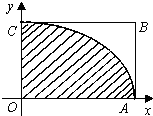    6．如图，曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1（0≤x≤3，0≤y≤2），为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积，现采用随机模拟方式产生x∈（0，3），y∈（0，2）的200个点（x，y），经统计，落在图中阴影部分的点共157个，则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84．（精确到0.01）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，短轴一个端点到右焦点的距离为2，直线l过点P（-1，0）且与曲线C交于A，B两点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）△AOB的面积是否存在最大值，若存在，求出△AOB的面积，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若直线x+2y-3=0，kx+y-1=0，x轴的正半轴和y轴的正半轴所围成的四边形有外接圆，且k＜0，则实数k的值为-2．

    查看答案和解析>>

    同步练习册答案