
| A£® | ³ä·Ö²»±Ø̉ª | B£® | ±Ø̉ª²»³ä·Ö | ||
| C£® | ³ä̉ª | D£® | ¼È²»³ä·Ö̉²²»±Ø̉ª |
·ÖÎö ÀûÓĂỊ̈Á¿¹²ÏߵĶ¨̉å¼°Ị̈Á¿µÄÊưÁ¿»ư¹«Ê½̉Ô¼°³ä̉ª̀ơ¼₫µÄ¶¨̉å¼´¿ÉÅĐ¶Ï£®
½â´đ ½â£ºÈô|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•|cos¦È|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|£¬¹Ê¦È=0¡ă»̣180¡ă£¬¹Ê¡°$\overrightarrow{a}$Óë$\overrightarrow{b}$¹²Ïߣ¬
Èô¹Ê¡°$\overrightarrow{a}$Óë$\overrightarrow{b}$¹²Ïߣ¬Ộ¡°$\overrightarrow{a}$Óë$\overrightarrow{b}$¹²¼Đ½ÇµÄÓàÏ̉Ϊ¡À1µÈ¼ÛÓÚ£º|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|£¬
¹ÊÉèỊ̈Á¿$\overrightarrow{a}$¡¢$\overrightarrow{b}$£¬Ộ¡°|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|¡±ÊÇ¡°$\overrightarrow{a}$Óë$\overrightarrow{b}$¹²Ïß¡±µÄ³ä̉ª̀ơ¼₫£¬
¹ÊÑ¡£ºC£®
µăÆÀ ±¾̀⿼²éỊ̈Á¿¹²Ïߵijä̉ª̀ơ¼₫¡¢Ị̈Á¿¹²ÏߵĶ¨̉å¡¢Ị̈Á¿¹²ÏßµÄ×ø±êĐÎʽµÄ³ä̉ª̀ơ¼₫£®


 º®¼ÙѧÓëÁ·ÏµÁĐ´đ°¸
º®¼ÙѧÓëÁ·ÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 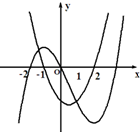 | B£® | 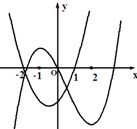 | C£® |  | D£® |  |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
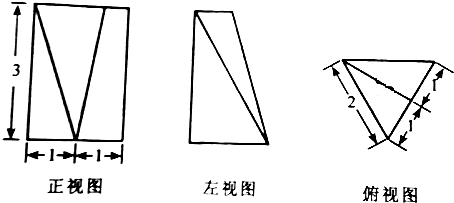
| A£® | $\frac{3\sqrt{3}}{2}$ | B£® | 2$\sqrt{3}$ | C£® | $\frac{5\sqrt{3}}{2}$ | D£® | 3$\sqrt{3}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com