
| A. | 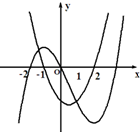 | B. | 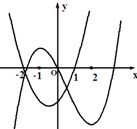 | C. |  | D. |  |
分析 利用导数与函数之间的关系.把握住导数的正负确定出函数的单调区间,根据变化趋势选出恰当的图象.确定出答案.
解答 解:∵f(x)=2ax3-3ax2-12ax(a≠0),
∴g(x)=f′(x)=6ax2-6ax-12a=6a${(x-\frac{1}{2})}^{2}$-$\frac{27a}{2}$,
对称轴x=$\frac{1}{2}$,而f′(-1)=f′(2)=0,
根据f′(x)>0时,y=f(x)递增;f′(x)<0时,y=f(x)递减可得.
①中函数的图象的增减趋势与导函数的正负区间是吻合的,可能正确;
而②④中的对称轴不是$\frac{1}{2}$,③中函数的图象的增减趋势与导函数的正负区间不吻合,故错误,
故选:A.
点评 本题考查函数与其导函数的关系,函数的递增区间即为导函数为正的区间,函数的递减区间即为导函数为负的区间,根据这个依赖性可以确定出函数图形吻合的是哪一个.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数y=f(x),其导函数y=f′(x)的图象如图所示,则y=f(x)( )
已知函数y=f(x),其导函数y=f′(x)的图象如图所示,则y=f(x)( )| A. | 在(-∞,0)上为减函数 | B. | 在x=1处取极小值 | ||
| C. | 在x=2处取极大值 | D. | 在(4,+∞)上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(-∞,1)上单调递增 | B. | 函数f(x)在(-∞,1)上单调递减 | ||
| C. | 函数f(x)在(-2,2)上单调递增 | D. | 函数f(x)在(-2,2)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)>e2f(0),f(2016)>e2016f(0) | B. | f(2)<e2f(0),f(2016)>e2016f(0) | ||
| C. | f(2)<e2f(0),f(2016)<e2016f(0) | D. | f(2)>e2f(0),f(2016)<e2016f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)>g(x) | B. | f(x)+g(3)<g(x)+f(3) | C. | f(x)<g(x) | D. | f(x)+g(7)<g(x)+f(7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com