练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)是奇函数，g(x)是偶函数，且f(－1)＋g(1)＝2，f(1)＋g(－1)＝4，则g(1)等于(　　)

    A．4                              B．3

    C．2                              D．1


    B　由已知可得，－f(1)＋g(1)＝2，

    f(1)＋g(1)＝4，两式相加解得，g(1)＝3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在命题p的四种形式(原命题、逆命题、否命题、逆否命题)中，真命题的个数记为f(p)，已知命题p：“若两条直线l1：a1x＋b1y＋c1＝0，l2：a2x＋b2y＋c2＝0平行，则a1b2－a2b1＝0”．那么f(p)等于(　　)

    A．1                                                   B．2

    C．3                                                   D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)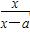＝(x≠a)．

    (1)若a＝－2，试证明f(x)在(－∞，－2)内单调递增；

    (2)若a>0且f(x)在(1，＋∞)内单调递减，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “无字证明”(proofs without words)，就是将数学命题用简单、有创意而且易于理解的几何图形来呈现．请利用图甲、图乙中阴影部分的面积关系，写出该图所验证的一个三角恒等变换公式：                                          ．

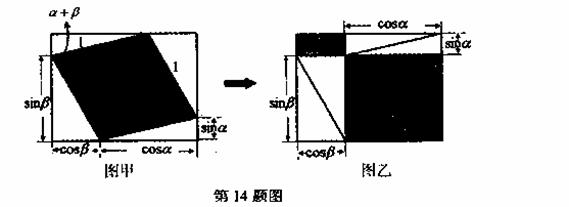
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知.

       （1）若 ，函数在其定义域内是增函数，求的取值范围；

       （2）当，时，证明函数只有一个零点；

       （3）的图象与轴交于, ()两点，中点为，

            求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)，g(x)分别是定义在R上的奇函数和偶函数，且f(x)－g(x)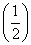＝x，则f(1)，g(0)，g(－1)之间的大小关系是______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的图像大致是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝x2－ax－a在区间[0,2]上的最大值为1，则实数a等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于定义域为D的函数f(x)，若存在区间M＝[a，b]⊆D(a<b)，使得{y|y＝f(x)，x∈M}＝M，则称区间M为函数f(x)的“等值区间”．给出下列四个函数：

    ①f(x)＝2x；②f(x)＝x3；③f(x)＝sin x；④f(x)＝log2x＋1.

    则存在“等值区间”的函数是________．(把正确的序号都填上)

    查看答案和解析>>

    同步练习册答案