
如图,已知直线 与抛物线
与抛物线 相切于点
相切于点 ,且与
,且与 轴交于点
轴交于点 ,
, 为坐标原点,定点
为坐标原点,定点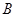 的坐标为
的坐标为 .
.

(1)若动点 满足
满足 ,求点
,求点 的轨迹
的轨迹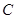 ;
;
(2)若过点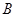 的直线
的直线 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹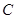 交于不同的两点
交于不同的两点 (
( 在
在 之间),试求△OBE与△OBF面积之比的取值范围.
之间),试求△OBE与△OBF面积之比的取值范围.
(I)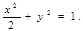 点M的轨迹为以原点为中心,焦点在x轴上,长轴长为
点M的轨迹为以原点为中心,焦点在x轴上,长轴长为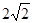 ,短轴长为2的椭圆
,短轴长为2的椭圆
(II)(3-2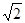 , 1)
, 1)
【解析】
试题分析:(I)由 ,
, ∴直线l的斜率为
∴直线l的斜率为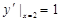 ,
,
故l的方程为 ,∴点A坐标为(1,0)
,∴点A坐标为(1,0)
设 则
则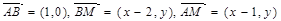 ,
,
由 得
得 
整理,得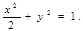
∴点M的轨迹为以原点为中心,焦点在x轴上,长轴长为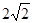 ,短轴长为2的椭圆
,短轴长为2的椭圆
(II)如图,由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①
将①代入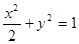 ,整理,得
,整理,得

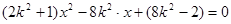 ,
,
由△>0得0<k2<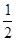 . 设E(x1,y1),F(x2,y2)
. 设E(x1,y1),F(x2,y2)
则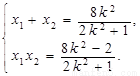 ② 令
② 令 ,由此可得
,由此可得
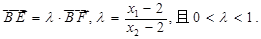
由②知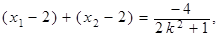

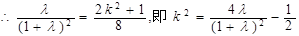
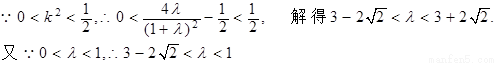
∴△OBE与△OBF面积之比的取值范围是(3-2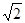 , 1)
, 1)
考点:本题主要考查椭圆标准方程,直线与椭圆的位置关系,平面向量的坐标运算,简单不等式解法。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用“直接法”,将向量关系用坐标表示,达到解题目的。(2)作为研究直线与椭圆位置关系下,三角形面积之比的范围问题,应用韦达定理及向量,建立了 的不等式,进一步使问题得解。
的不等式,进一步使问题得解。


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省桐乡市高三10月月考文科数学 题型:填空题
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆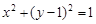 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求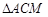 与
与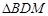 面积之和的最小值.
面积之和的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三第二次月考文科数学 题型:解答题
(本题满分18分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
(Ⅲ)过A、B分别作抛物C的切线 且
且 交于点M,求
交于点M,求 与
与 面积之和的最小值.
面积之和的最小值.

查看答案和解析>>
科目:高中数学 来源:山东省月考题 题型:解答题
 |BD|为定值;
|BD|为定值;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com