
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)
为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)| 身高(cm) | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
| 人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的虚部为3i | |
| B. | z的共轭复数为1-3i | |
| C. | |z|=4 | |
| D. | z在复平面内对应的点在第三象限内 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
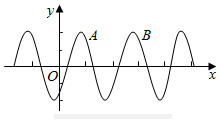 已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示,若A($\frac{π}{2}$,$\sqrt{2}$),B($\frac{3π}{2}$,$\sqrt{2}$).则下列说法错误的是( )
已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示,若A($\frac{π}{2}$,$\sqrt{2}$),B($\frac{3π}{2}$,$\sqrt{2}$).则下列说法错误的是( )| A. | φ=$\frac{3π}{4}$ | |
| B. | 函数f(x)的一条对称轴为x=$\frac{15π}{8}$ | |
| C. | 为了得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移$\frac{π}{8}$个单位 | |
| D. | 函数f(x)的一个单调减区间为[$\frac{9π}{8}$,$\frac{13π}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com