练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．求实数m取什么值时，复平面内表示复数z=（m2-8m+15）+（m2-5m-14）i的点位于第四象限．

    分析 复平面内表示复数z=（m2-8m+15）+（m2-5m-14）i的点位于第四象限，可得m2-8m+15＞0，m2-5m-14＜0，利用一元二次不等式的解法即可得出．

    解答 解：∵复平面内表示复数z=（m2-8m+15）+（m2-5m-14）i的点位于第四象限，
    ∴m2-8m+15＞0，m2-5m-14＜0，
    联立分别解得：m＞5或m＜3，-2＜m＜7．
    ∴-2＜m＜3，或5＜m＜7．
    ∴当-2＜m＜3，或5＜m＜7时，复平面内表示复数z=（m2-8m+15）+（m2-5m-14）i的点位于第四象限．

    点评 本题考查了复数的几何意义、一元二次不等式的解法，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．$\lim_{△x→0}\frac{{cos（\frac{π}{6}+△x）-cos\frac{π}{6}}}{△x}$的值为$-\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．“a＞3”是“函数f（x）=x2-2ax-2在区间（-∞，2]内单调递减”的（　　）
    A．充分非必要条件B．必要非充分条件
    C．充要条件D．既不充分也必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若a，b∈R，则复数（a2-4a+5）+（-b2+2b-6）i所对应的点一定落在第四象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

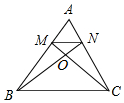    1．如图，在△ABC中，MN∥BC，$\frac{AM}{MB}$=$\frac{1}{2}$，MC，NB交于点O，若△OMN的面积等于a，得△OBC的面积等于9a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知三个不等式：①ab＞0；②bc＞ad；③$\frac{c}{a}＞\frac{d}{b}$．以其中两个作为条件，余下一个作为结论，则可以组成正确命题的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

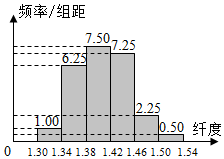    18．在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，将数据分组如表（频率分布表），并画出了频率分布直方图．
    （1）估计纤度落在[1.38，1.50）的概率及纤度小于1.40的概率；
    （2）从频率分布直方图估计出纤度的众数，中位数和平均数．
    分 组频 数频 率
    [1.30，1.34）40.04
    [1.34，1.38）250.25
    [1.38，1.42）300.30
    [1.42，1.46）290.29
    [1.46，1.50）100.10
    [1.50，1.54]20.02
    合 计1001

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在10件产品中，有3件一等品，7件二等品，从这10件产品中任取3件，则取出的3件产品中一等品件数多于二等品件数的概率（　　）
    A．$\frac{1}{120}$B．$\frac{7}{40}$C．$\frac{11}{60}$D．$\frac{21}{40}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．函数y=$\sqrt{8-{2^x}_{\;}}$的值域是（　　）
    A．[0，+∞）B．$[{0，2\sqrt{2}}]$C．$（{0，2\sqrt{2}}）$D．$[{0，2\sqrt{2}}）$

    查看答案和解析>>

    同步练习册答案