Question

8．（1）设G是△ABC的重心，证明：△GBC，△GAC，△GAB的面积相等．
（2）利用（1）的结论，证明：三角形顶点到重心的距离，等于重心到对边中点的距离的2倍．

Answer 1

分析 （1）设三条中线为AD，BE，CF，三中线交于G点，G是重心，由同底等高得到S_△GBC=2S_△GCD，S_△GAC=2S_△GCD，由此能证明△GBC，△GAC，△GAB的面积相等．
（2）设三条中线为AD，BE，CF，三中线交于G点，G是重心，由S_△GBC=S_△GAC，S_△GBC=2S_△GCD，得到S_△GAC=2S_△GCD，由此能证明三角形顶点到重心的距离，等于重心到对边中点的距离的2倍．

解答 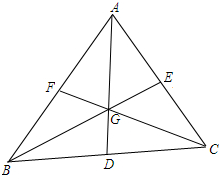（1）证明：设三条中线为AD，BE，CF，三中线交于G点，G是重心，
则AG=2GD，CG=2GF，BG=2GE，
∵BD=CD，∴S_△GBC=2S_△GCD，
∵AG=2GD，∴S_△GAC=2S_△GCD，
∴S_△GBC=S_△GAC，
同理S_△GAC=S_△GAB，
∴△GBC，△GAC，△GAB的面积相等．
（2）证明：设三条中线为AD，BE，CF，三中线交于G点，G是重心，
∵△GBC，△GAC，△GAB的面积相等，
∴S_△GBC=S_△GAC，
∵BD=CD，∴S_△GBC=2S_△GCD，
∴S_△GAC=2S_△GCD，
∵△AGC和△DGC在分别以AG和DG为底时，高都是点C到边AD的距离，
∴AG=2GD，同理可证CG=2GF，BG=2GE，
∴三角形顶点到重心的距离，等于重心到对边中点的距离的2倍．

点评 本题考查三角形面积相等的证明，考查三角形重心定理的证明，是中档题，解题时要注意三角形面积公式的合理运用．