
分析 (1)f′(x)=-aln(x+1)+$\frac{1-ax}{x+1}$-b,根据条件知f′(0)=0,解出即可.
(2)由(1)得f(x)=(1-ax)ln(1+x)-x,0≤x≤1.f′(x)-aln(x+1)+$\frac{1-ax}{1+x}$-1,令g(x)=f′(x),g′(x)=-$\frac{ax+2a+1}{(1+x)^{2}}$.对a分类讨论,研究函数g(x)的单调性极值与最值,进而得出函数f(x)的极值与最值.
解答 解:(1)f′(x)=-aln(x+1)+$\frac{1-ax}{x+1}$-b,
根据条件知f′(0)=0,
∴1-b=0,解得b=1.
(2)由(1)得f(x)=(1-ax)ln(1+x)-x,0≤x≤1.
f′(x)-aln(x+1)+$\frac{1-ax}{1+x}$-1,
令g(x)=f′(x),
g′(x)=$\frac{-a}{x+1}$+$\frac{-a(1+x)-(1-ax)}{(1+x)^{2}}$=-$\frac{ax+2a+1}{(1+x)^{2}}$.
①当a≤$-\frac{1}{2}$时,由于0≤x≤1,有g′(x)=-$\frac{a(x+\frac{2a+1}{a})}{(1+x)^{2}}$≥0,于是f′(x)在[0,1]上单调递增,从而f′(x)≥f′(0)=0,因此f(x)在[0,1]上单调递增,
即f(x)≥f(0)=0,而且仅有f(0)=0;
②当a≥0时,由于0≤x≤1,有g′(x)=$-\frac{ax+2a+1}{(1+x)^{2}}$<0,于是f′(x)在[0,1]上单调递减,从而f′(x)≤f′(0)=0,因此f(x)在[0,1]上单调递减.
即f(x)≤f(0)=0,而且仅有f(0)=0;
③当$-\frac{1}{2}<a<0$时,令m=min$\{1,-\frac{2a+1}{a}\}$,当0≤x≤m时,g′(x)≤0,于是f′(x)在[0,m]上单调递减,从而f′(x)≤f′(0)=0,因此f(x)在[0,m]上单调递减,
即f(x)≤f(0)=0,而且仅有f(0)=0.
综上可知,所求实数a的取值范围是$(-∞,-\frac{1}{2}]$.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,已知面ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
如图,在多面体ABCDEF中,已知面ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
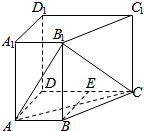 如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.
如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$ | B. | 32 | C. | $\frac{64\sqrt{3}}{9}$ | D. | $\frac{128\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.
已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com