
分析 (Ⅰ)由题意可知,数列{n+3n-1}是由等比数列与等差数列和的形式,根据等比数列和等差数列前n项和公式,即可求得Sn;
(Ⅱ)数列{n×3n-1}是由等比数列和等差数列的乘积组成的数列,采用“错位相减法”即可求得Tn.
解答 解:(1)由Sn=1+2+3+…+n+1+3+32+33+…+3n-1
=$\frac{n(n+1)}{2}$+$\frac{1-{3}^{n-1}•3}{1-3}$
=$\frac{{3}^{n}+{n}^{2}+n-1}{2}$,
∴Sn=$\frac{{3}^{n}+{n}^{2}+n-1}{2}$;
(2)Tn=1×1+2×3+3×32+…+n×3n-1,
∴3Tn=1×3+2×32+3×33+…+n×3n,
两式相减:-2Tn=1+3+32+…+3n-1-n×3n,
=$\frac{1-{3}^{n-1}•3}{1-3}$-n×3n,
=$\frac{(2n-1)•{3}^{2}+1}{4}$.
∴Tn=$\frac{(2n-1)•{3}^{2}+1}{4}$.
点评 本题考查等差数列和等比数列前n项和公式,考查“错位相减法”求数列的前n项方法,考查计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
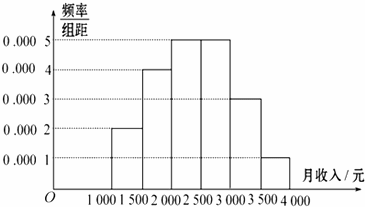
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
| A. | 0.44 | B. | 0.56 | C. | 0.86 | D. | 0.14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(理)试卷(解析版) 题型:解答题
已知椭圆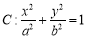
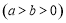 的焦距为2,离心率为
的焦距为2,离心率为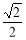 ,
,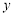 轴上一点
轴上一点 的坐标为
的坐标为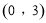 .
.
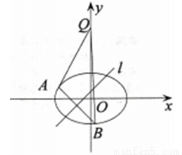
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线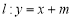 ,椭圆
,椭圆 上总存在不同的两点
上总存在不同的两点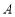 与
与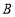 关于直线
关于直线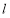 对称,且
对称,且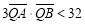 ,求
,求
实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com