【题目】定义在
上的偶函数
满足
，当
时，
，设函数
，则与
的图象所有交点的横坐标之和为（ ）．
A. 3B. 4C. 5D. 6
【答案】B
【解析】
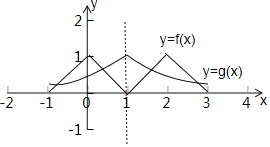
由函数图象的性质得：f（x）的图象关于直线x＝1对称且关于y轴对称，函数g（x）＝e﹣|x﹣1|（﹣1＜x＜3）的图象也关于直线x＝1对称，由函数图象的作法可知两个图象有四个交点，且两两关于直线x＝1对称，则f（x）与g（x）的图象所有交点的横坐标之和为4，得解
由偶函数f（x）满足 （1+x）＝f （1﹣x）可得f（x）的图象关于直线x＝1对称且关于y轴对称，
函数g（x）＝e﹣|x﹣1|（﹣1＜x＜3）的图象也关于直线x＝1对称，
函数y＝f（x）的图象与函数g（x）＝e﹣|x﹣1|（﹣1＜x＜3）的图象的位置关系如图所示，
可知两个图象有四个交点，且两两关于直线x＝1对称，
则f（x）与g（x）的图象所有交点的横坐标之和为4，
故选：B．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】洛萨·科拉茨是德国数学家，他在1937年提出了一个著名的猜想：任给一个正整数
，如果是偶数，就将它减半（即
）；如果是奇数，则将它乘3加1（即
），不断重复这样的运算，经过有限步后，一定可以得到1，如初始正整数为6，按照上述变换规则，我们得到一个数列：6,3,10,5,16,8,4,2,1.对科拉茨猜想，目前谁也不能证明，更不能否定，如果对正整数按照上述规则实施变换（注：1可以多次出现）后的第九项为1，则的所有可能取值的集合为_________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）六个从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有几种？
（2）把5件不同产品摆成一排，若产品
与产品
相邻，且产品与产品
不相邻，则不同的摆法有几种？
（3）某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法有几种？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知三棱柱BCF﹣ADE的侧面CFED与ABFE都是边长为1的正方形，M、N两点分别在AF和CE上，且AM=EN．
（1）求证：平面ABCD⊥平面ADE；
（2）求证：MN∥平面BCF；
（3）若点N为EC的中点，点P为EF上的动点，试求PA+PN的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=-sin2x+mcosx-1，x∈[
]．
（1）若f（x）的最小值为-4，求m的值；
（2）当m=2时，若对任意x1，x2∈[-
]都有|f（x1）-f（x2）|
恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的离心率为
，
，
为其左、右顶点，
为椭圆上除，外任意一点，若记直线
，
斜率分别为
，
.
（1）求证：
为定值；
（2）若椭圆的长轴长为4，过点
作两条互相垂直的直线
，
，若
恰好为与椭圆相交的弦的中点，求与椭圆相交的弦的中点的横坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C：x2+y2+x-6y+m=0与直线l：x+2y-3=0．
（1）若直线l与圆C没有公共点，求m的取值范围；
（2）若直线l与圆C相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
