
【题目】已知圆C:x2+y2+x-6y+m=0与直线l:x+2y-3=0.
(1)若直线l与圆C没有公共点,求m的取值范围;
(2)若直线l与圆C相交于P、Q两点,O为原点,且OP⊥OQ,求实数m的值.
【答案】(1)![]() (2)m=3
(2)m=3
【解析】
(1)将圆的方程配方,
得![]() 2+(y-3)2=
2+(y-3)2=![]() ,
,
故有![]() >0,解得m<
>0,解得m<![]() .
.
将直线l的方程与圆C的方程组成方程组,得![]()
消去y,得x2+![]() 2+x-6×
2+x-6×![]() +m=0,
+m=0,
整理,得5x2+10x+4m-27=0, ①
∵直线l与圆C没有公共点,∴方程①无解,故有Δ=102-4×5(4m-27)<0,解得m>8.∴m的取值范围是![]() .
.
(2)设P(x1,y1),Q(x2,y2),
由OP⊥OQ,得![]() =0,即x1x2+y1y2=0, ②
=0,即x1x2+y1y2=0, ②
由①及根与系数的关系,得
x1+x2=-2,x1·x2=![]() , ③
, ③
又∵P、Q在直线x+2y-3=0上,
∴y1·y2=![]() ·
·![]() =
=![]() [9-3(x1+x2)+x1·x2],
[9-3(x1+x2)+x1·x2],
将③代入上式,得y1·y2=![]() , ④
, ④
将③④代入②得x1·x2+y1·y2=![]() +
+![]() =0,解得m=3.
=0,解得m=3.
代入方程①检验得Δ>0成立,∴m=3.


科目:高中数学 来源: 题型:
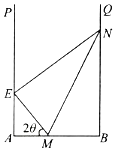
【题目】某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分隔线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分隔线总长度为l.
(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A.f(x)= ![]()
B.f(x)=x3
C.f(x)=( ![]() )x
)x
D.f(x)=3x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( ) 
A.y= ![]() ﹣
﹣ ![]() x
x
B.y= ![]() x3﹣
x3﹣ ![]() x
x
C.y= ![]() x3﹣x
x3﹣x
D.y=﹣ ![]() x3+
x3+ ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是( )
A.[﹣5,﹣3]
B.[﹣6,﹣ ![]() ]
]
C.[﹣6,﹣2]
D.[﹣4,﹣3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com