
【题目】(1)六个从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有几种?
(2)把5件不同产品摆成一排,若产品![]() 与产品
与产品![]() 相邻,且产品
相邻,且产品![]() 与产品
与产品![]() 不相邻,则不同的摆法有几种?
不相邻,则不同的摆法有几种?
(3)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法有几种?
【答案】(1)216(2)36(3)120
【解析】分析:(1)分两种情况讨论甲在最左端时,有![]() ,当甲不在最左端时,有
,当甲不在最左端时,有![]() (种)排法,由分类计数加法原理可得结果;(2)分三步:将
(种)排法,由分类计数加法原理可得结果;(2)分三步:将![]() 看成一个整体,将
看成一个整体,将![]() 于剩余的2件产品全排列,
于剩余的2件产品全排列,![]() 有3个空位可选,根据分步计数乘法原理可得结果;(3)用
有3个空位可选,根据分步计数乘法原理可得结果;(3)用![]() 表示歌舞类节目,小品类节目,相声类节目,利用枚举法可得共有
表示歌舞类节目,小品类节目,相声类节目,利用枚举法可得共有![]() 种,每一种排法种的三个
种,每一种排法种的三个![]() ,两个
,两个![]() 可以交换位置,故总的排法为
可以交换位置,故总的排法为![]() 种.
种.
详解:(1)当甲在最左端时,有![]() ;当甲不在最左端时,乙必须在最左端,且甲也不在最右端,有
;当甲不在最左端时,乙必须在最左端,且甲也不在最右端,有![]() (种)排法,共计
(种)排法,共计![]() (种)排法.
(种)排法.
(2)根据题意,分3步进行分析:
产品![]() 与产品
与产品![]() 相邻,将
相邻,将![]() 看成一个整体,考虑
看成一个整体,考虑![]() 之间的顺序,有
之间的顺序,有![]() 种情况,
种情况,
将![]() 于剩余的2件产品全排列,有
于剩余的2件产品全排列,有![]() 种情况,
种情况,
产品![]() 与产品
与产品![]() 不相邻,
不相邻,![]() 有3个空位可选,即有3种情况,共有
有3个空位可选,即有3种情况,共有![]() 种;
种;
(3)法一:用![]() 表示歌舞类节目,小品类节目,相声类节目,则可以枚举出下列10种:
表示歌舞类节目,小品类节目,相声类节目,则可以枚举出下列10种:![]()
![]()
每一种排法种的三个![]() ,两个
,两个![]() 可以交换位置,故总的排法为
可以交换位置,故总的排法为![]() 种.
种.
法二:分两步进行:(1)先将3个歌曲进行全排,其排法有![]() 种;(2)将小品与相声插入将歌曲分开,若两歌舞之间只有一个其他节目,其插法有
种;(2)将小品与相声插入将歌曲分开,若两歌舞之间只有一个其他节目,其插法有![]() 种.若两歌舞之间有两个其他节目时插法有
种.若两歌舞之间有两个其他节目时插法有![]() 种.所以由计数原理可得节目的排法共有
种.所以由计数原理可得节目的排法共有![]() (种).
(种).


科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的标准方程为
的标准方程为![]() ,
,![]() 为圆
为圆![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() ,动点
,动点![]() 在直线
在直线![]() 上.
上.
(1)求![]() 的最小值,并求此时点
的最小值,并求此时点![]() 的坐标;
的坐标;
(2)若![]() 点的坐标为
点的坐标为![]() ,过
,过![]() 作直线与圆
作直线与圆![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某植物园准备建一个五边形区域的盆栽馆,三角形ABE为盆裁展示区,沿AB、AE修建观赏长廊,四边形BCDE是盆栽养护区,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
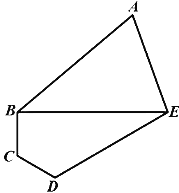
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求观赏长廊总长度AB+AE的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其图像的一个对称中心是
其图像的一个对称中心是![]() 将
将![]() 的图像向左平移
的图像向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像。
的图像。
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() 当
当![]() 时,都有
时,都有![]() 求实数
求实数![]() 的最大值;
的最大值;
(3)若对任意实数![]() 在
在![]() 上与直线
上与直线![]() 的交点个数不少于6个且不多于10个,求正实数
的交点个数不少于6个且不多于10个,求正实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一块大型的广告宣传版面,其形状是右图所示的直角梯形![]() .某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
, ![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.

(1)建立适当的平面直角坐标系,分别求出曲线段![]() 与线段
与线段![]() 的方程;
的方程;
(2)求该厂家广告区域![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
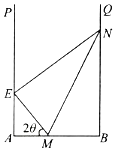
【题目】某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分隔线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分隔线总长度为l.
(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com