
分析 要证原不等式成立,可证n+(1+$\frac{1}{2}$+…+$\frac{1}{n}$)=(1+1)+(1+$\frac{1}{2}$)+…+(1+$\frac{1}{n}$)>n$\root{n}{n+1}$,运用均值不等式即可得证.
解答 证明:n+(1+$\frac{1}{2}$+…+$\frac{1}{n}$)=(1+1)+(1+$\frac{1}{2}$)+…+(1+$\frac{1}{n}$)
=2+$\frac{3}{2}$+…+$\frac{n+1}{n}$>n$\root{n}{2•\frac{3}{2}…\frac{n+1}{n}}$=n$\root{n}{n+1}$,
即有1+$\frac{1}{2}$+…+$\frac{1}{n}$>n$\root{n}{n+1}$-n,
即为$\frac{1}{n}$(1+$\frac{1}{2}$+…+$\frac{1}{n}$)>$\root{n}{n+1}$-1(n∈N+,n>1).
点评 本题考查不等式的证明,重点考查均值不等式的运用,注意化简整理,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6$+2\sqrt{2}$ | B. | 6$+2\sqrt{3}$ | C. | 6$+\sqrt{2}$ | D. | 6$+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.
如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
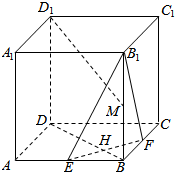 如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:
如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“p或q”为假 | B. | 命题“p且q“为真 | ||
| C. | 命题,“¬p或q”为假 | D. | 命题“p且¬q“为假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com