
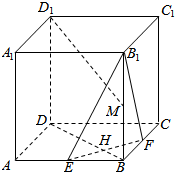
 如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:
如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:分析 (1)证明EF垂直于BD,DD1,即可证明EF⊥平面BB1D1D;
(2)证明FB1⊥平面D1C1M,即可证明平面EFB1⊥平面D1C1M.
解答  证明:(1)∵E、F分别为AB和BC的中点,
证明:(1)∵E、F分别为AB和BC的中点,
∴EF∥AC,
∵AC⊥BD,
∴EF⊥BD,
∵DD1⊥平面ABCD,EF?平面ABCD,
∴DD1⊥EF,
∵DD1∩BD=D,
∴EF⊥平面BB1D1D;
(2)由△B1C1M≌△BB1F,可得FB1⊥C1M.
再由D1C1⊥平面BCC1B1,可得FB1⊥D1C1,
∵C1M∩D1C1=C1,
∴FB1⊥平面D1C1M,
∵FB1?平面EFB1,
∴平面EFB1⊥平面D1C1M.
点评 本题考查线面垂直、面面垂直的判定,考查学生分析解决问题的能力,正确证明线面垂直是关键.


科目:高中数学 来源: 题型:解答题
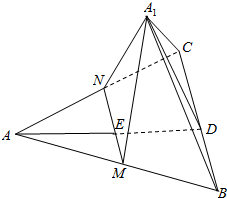 如图,AD为△ABC的边BC上的高,E在AD上,且ED=2AE,过E作直线MN∥BC,分别交AB,AC于M,N点,将△AMN沿MN折起到A1MN,使二面角A1-MN-C为60°,求证:平面A1MN⊥平面A1BC.
如图,AD为△ABC的边BC上的高,E在AD上,且ED=2AE,过E作直线MN∥BC,分别交AB,AC于M,N点,将△AMN沿MN折起到A1MN,使二面角A1-MN-C为60°,求证:平面A1MN⊥平面A1BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.
如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com