
【题目】已知函数 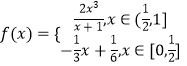 ,函数
,函数 ![]()
![]() (a>0),若存在
(a>0),若存在 ![]() ,使得
,使得 ![]() 成立,则实数
成立,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】∵ 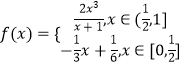 ,
,
① 当x∈[0, ![]() ]时,f(x)=
]时,f(x)= ![]() 在R上是单调递减函数,
在R上是单调递减函数,
∴f( ![]() )f(x)f(0),即0f(x)
)f(x)f(0),即0f(x) ![]() ,
,
∴f(x)的值域为[0, ![]() ];
];
② 当x∈( ![]() ,1]时,f(x)=
,1]时,f(x)= ![]() ,
,
∴f′(x)= ![]() =
= ![]() ,
,
∴当x> ![]() 时,f′(x)>0,即f(x)在(
时,f′(x)>0,即f(x)在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴f(x)在( ![]() ,1]上单调递增,
,1]上单调递增,
∴f( ![]() )<f(x)f(1),即
)<f(x)f(1),即 ![]() <f(x)1,
<f(x)1,
∴f(x)的值域为[ ![]() ,1].
,1].
综合①②,f(x)的值域为[0,1].
∵g(x)=asin( ![]() )2a+2,(a>0),且x∈[0,1],
)2a+2,(a>0),且x∈[0,1],
∴0 ![]() x
x ![]() ,则0sin(
,则0sin( ![]() x)
x) ![]() ,
,
∵a>0则0asin( ![]() x)
x) ![]() a,
a,
∴22ag(x)2 ![]() a,
a,
∴g(x)的值域为[22a,2 ![]() a],
a],
∵存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,
∴[0,1]∩[22a,2 ![]() a]≠,
a]≠,
若[0,1]∩[22a,2 ![]() a]=,则2
a]=,则2 ![]() a<0或22a>1,
a<0或22a>1,
∴a< ![]() 或a>
或a> ![]() ,
,
∴当[0,1]∩[22a,2 ![]() a]≠时,a的取值范围为[12,
a]≠时,a的取值范围为[12, ![]() ],
],
∴实数a的取值范围是[ ![]() ,
, ![]() ].
].
故答案为:D.
根据x的范围确定函数的值域和 g(x) 的值域,进而根据f ( x1 ) = g ( x2 ) 成立,推断出[0,1]∩[22a,2 3 2 a]≠时,先看当二者的交集为空集时求得a的范围,故可求得当集合的交集为非空时a的范围。


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼,随机抽取50条作为样本进行统计,按海鱼重量(克)得到如图的频率分布直方图: 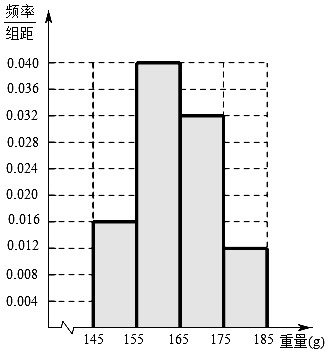
(Ⅰ)若经销商购进这批海鱼100千克,试估计这批海鱼有多少条(同一组中的数据用该区间的中点值作代表);
(Ⅱ)根据市场行情,该海鱼按重量可分为三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [165,185] | [155,165) | [145,155) |
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据,视频率为概率.现从这批海鱼中随机抽取3条,记抽到二等品的条数为X,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程.
的一元二次方程. ![]() .
.
(1)若![]() 是从0、1、2、3四个数中任取的一个数,
是从0、1、2、3四个数中任取的一个数, ![]() 是从0、1、2三个数中任取的一个数,求上述方程有实数根的概率;
是从0、1、2三个数中任取的一个数,求上述方程有实数根的概率;
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数, ![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实数根的概率.
任取的一个数,求上述方程有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率. 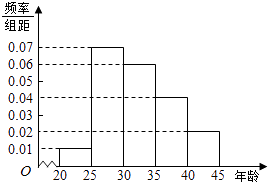
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线
中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,圆
,圆 ![]() 的极坐标方程是
的极坐标方程是 ![]() .
.
(1)求 ![]() 与
与 ![]() 交点的极坐标;
交点的极坐标;
(2)设 ![]() 为
为 ![]() 的圆心,
的圆心, ![]() 为
为 ![]() 与
与 ![]() 交点连线的中点,已知直线
交点连线的中点,已知直线 ![]() 的参数方程是
的参数方程是 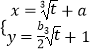 (
( ![]() 为参数),求
为参数),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.命题“ ![]() ,
, ![]() ”的否定是“
”的否定是“ ![]() ,
, ![]() ”
”
B.命题“ ![]() 为真”是命题“
为真”是命题“ ![]() 为真”的充分不必要条件
为真”的充分不必要条件
C.命题“若am2≤bm2 , 则a≤b”是假命题
D.命题“在中 ![]() 中,若
中,若 ![]() ,则
,则 ![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆![]() 的方程为
的方程为![]() ,点
,点![]() 为圆上的动点.
为圆上的动点.
(1)求过点![]() 的圆
的圆![]() 的切线方程.
的切线方程.
(2)求![]() 的最大值及此时对应的点
的最大值及此时对应的点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com