
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}为等比数列, ![]() 公比为
公比为![]()
![]() 为数列{an}的前n项和.
为数列{an}的前n项和.
(1)若![]() 求
求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数n,不等式
,使得对任意正整数n,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,函数
,函数![]() 定义于
定义于![]() 并取值于
并取值于![]() .(用数字作答)
.(用数字作答)
(1)若![]() 对于任意的
对于任意的![]() 成立,则这样的函数
成立,则这样的函数![]() 有_______个;
有_______个;
(2)若至少存在一个![]() ,使
,使![]() ,则这样的函数
,则这样的函数![]() 有____个.
有____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
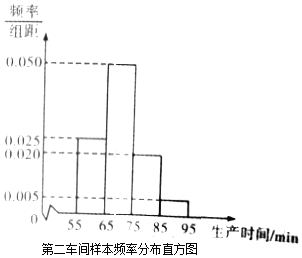
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
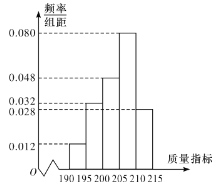
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ②函数
②函数![]() 有3个零点
有3个零点
③![]() 的解集为
的解集为![]() ④
④![]() ,都有
,都有![]()
其中正确命题的个数是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们要计算由抛物线![]() ,x轴以及直线
,x轴以及直线![]() 所围成的区域的面积S,可用x轴上的分点
所围成的区域的面积S,可用x轴上的分点![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、1将区间
、1将区间![]() 分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线
分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线![]() 上,这些矩形的高分别为
上,这些矩形的高分别为![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,矩形的底边长都是
,矩形的底边长都是![]() ,设所有这些矩形面积的总和为
,设所有这些矩形面积的总和为![]() ,为求S,只须令分割的份数n无限增大,
,为求S,只须令分割的份数n无限增大,![]() 就无限趋近于S,即
就无限趋近于S,即![]() .
.
(1)求数列![]() 的通项公式,并求出S;
的通项公式,并求出S;
(2)利用相同的思想方法,探求由函数![]()
![]() 的图象,x轴以及直线
的图象,x轴以及直线![]() 和
和![]() 所围成的区域的面积T.
所围成的区域的面积T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学进入新华书店购买数学课外阅读书籍,经过筛选后,他们都对![]() 三种书籍有购买意向,已知甲同学购买书籍
三种书籍有购买意向,已知甲同学购买书籍![]() 的概率分别为
的概率分别为![]() ,乙同学购买书籍
,乙同学购买书籍![]() 的概率分别为
的概率分别为![]() ,假设甲、乙是否购买
,假设甲、乙是否购买![]() 三种书籍相互独立.
三种书籍相互独立.
(1)求甲同学购买3种书籍的概率;
(2)设甲、乙同学购买2种书籍的人数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com