
【题目】已知集合![]() ,函数
,函数![]() 定义于
定义于![]() 并取值于
并取值于![]() .(用数字作答)
.(用数字作答)
(1)若![]() 对于任意的
对于任意的![]() 成立,则这样的函数
成立,则这样的函数![]() 有_______个;
有_______个;
(2)若至少存在一个![]() ,使
,使![]() ,则这样的函数
,则这样的函数![]() 有____个.
有____个.
【答案】15625 46575
【解析】
(1)若![]() 对于任意的
对于任意的![]() 成立,所以每一个
成立,所以每一个![]() ,可以对应除它本身之外5个元素之中的一个,利用分步乘法原理可得结果;
,可以对应除它本身之外5个元素之中的一个,利用分步乘法原理可得结果;
(2)从反面来研究,找到对任意在一个![]() ,使
,使![]() 的总数,然后用没有限制下的总数减去即可.
的总数,然后用没有限制下的总数减去即可.
(1)利用分步乘法原理,每一个![]() ,都有5种结果可以与它对应,
,都有5种结果可以与它对应,
故这样的函数有![]() 个;
个;
(2)若对任意在一个![]() ,使
,使![]() ,
,
①当集合![]() 中6个数都满足
中6个数都满足![]() 时,符合
时,符合![]() ,有1个;
,有1个;
②当集合![]() 中6个数有三个数满足
中6个数有三个数满足![]() ,
,![]() 两两不等时,另三个数满足
两两不等时,另三个数满足![]() ,符合
,符合![]() ,此时有
,此时有![]() 个;
个;
③当集合![]() 中6个数三个数满足
中6个数三个数满足![]() ,
,![]() 两两不等,另三个数也满足
两两不等,另三个数也满足![]() ,
,![]() 两两不等时,
两两不等时,
符合![]() ,此时有
,此时有![]() .
.
故若对任意一个![]() ,使
,使![]() ,这样的函数有81个,
,这样的函数有81个,
若至少存在一个![]() ,使
,使![]() ,则这样的函数
,则这样的函数![]() 有
有![]() 个.
个.
故答案为:15625;46575.


科目:高中数学 来源: 题型:
【题目】如图,内接于圆![]() 的正方形
的正方形![]() 边长为1,圆
边长为1,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,···,正方形
,···,正方形![]() 内接于圆
内接于圆![]() ,圆
,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,由此无穷个步骤进行下去记圆
,由此无穷个步骤进行下去记圆![]() 的面积记作
的面积记作![]() ,记正方形
,记正方形![]() 的面积记作
的面积记作![]() .
.
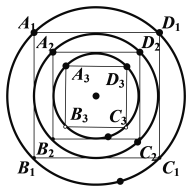
(1)求![]() 的值
的值
(2)记![]() 的所有项和为
的所有项和为![]() ,
,![]() 的所有项和为
的所有项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位全体员工年龄频率分布表,经统计,该单位35岁以下的青年职工中,男职工和女职工人数相等,且男职工的年龄频率分布直方图和如下:
年龄(岁) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55) | 合计 |
人数(人) | 6 | 18 | 50 | 31 | 19 | 16 | 140 |
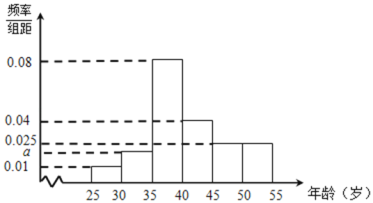
(Ⅰ)求![]() ;
;
(Ⅱ)求该单位男女职工的比例;
(Ⅲ)若从年龄在[25,30)岁的职工中随机抽取两人参加某项活动,求恰好抽取一名男职工和一名女职工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.
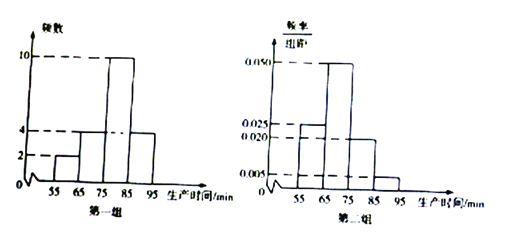
![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有标号为![]() 的
的![]() 张标签,随机的选取两张标签.
张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中
①.对于命题![]() :存在
:存在![]() ,则
,则![]() :
:![]() ;
;
②.命题“若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数”的逆命题为假命题;
上是增函数”的逆命题为假命题;
③.若![]() 为真命题,则
为真命题,则![]() 均为真命题;
均为真命题;
④.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”.
”.
错误的是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com