
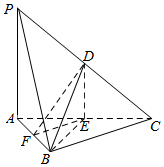
 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=BC=4,DF=2$\sqrt{2}$.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=BC=4,DF=2$\sqrt{2}$.分析 (1)根据中位线定理可得DE=EF=2,利用勾股定理的逆定理得出DE⊥EF,从而PA⊥EF,结合PA⊥AC得出PA⊥平面ABC;
(2)根据中点的性质得出△BEF和△ABC的面积比,DE与PA的比值,带入棱锥的体积公式得出体积比.
解答  证明:(1)∵D,E,F分别为棱PC,AC,AB的中点,
证明:(1)∵D,E,F分别为棱PC,AC,AB的中点,
∴DE∥PA,$DE=\frac{1}{2}PA=2$,$EF=\frac{1}{2}BC=2$,
∴DE2+EF2=DF2,∴DE⊥EF,
∴PA⊥EF,
又PA⊥AC,AC?平面ABC,EF?平面ABC,AC∩EF=E,
∴PA⊥平面ABC.
(2)∵D,E,F是PC,AC,AB的中点,
∴S△BEF=$\frac{1}{4}$S△ABC,DE=$\frac{1}{2}PA$.
∴VD-BEF=$\frac{1}{3}{S}_{△BEF}•DE$,
VP-ABC=$\frac{1}{3}{S}_{△ABC}•PA$=$\frac{1}{3}•4{S}_{△BEF}•2DE$=$\frac{8}{3}$S△BEF•DE.
∴$\frac{{V}_{D-BEF}}{{V}_{P-ABC}}=\frac{1}{8}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 2 | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 焦点为F的抛物线C:y2=2px(p>0)上有一动点P,且点P到抛物线C的准线与点D(0,2)的距离之和的最小值为$\sqrt{5}$
焦点为F的抛物线C:y2=2px(p>0)上有一动点P,且点P到抛物线C的准线与点D(0,2)的距离之和的最小值为$\sqrt{5}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为$\sqrt{3}$、$\frac{1}{10}$、e和$\frac{3}{5}$.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红.眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?
欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为$\sqrt{3}$、$\frac{1}{10}$、e和$\frac{3}{5}$.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红.眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分而不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>-2 | B. | m>-4 | C. | m<-2 | D. | m<-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com