
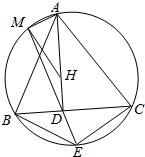
 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$,直线ED交外接圆于点M,求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$,直线ED交外接圆于点M,求证:∠AMH=90°. 分析 作高BP,CQ.连结MB、MC、MP、MQ、PQ.构建相似三角形△MBQ∽△MCP,从而推知点M、A、P、Q、H五点共圆,最后根据圆周角定理证得结论.
解答 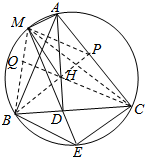 证明:作高BP,CQ.连结MB、MC、MP、MQ、PQ.
证明:作高BP,CQ.连结MB、MC、MP、MQ、PQ.
$\frac{BD}{DC}$=$\frac{{S}_{△BME}}{{S}_{△CME}}$=$\frac{\frac{1}{2}BM•BE•sin∠MBE}{\frac{1}{2}CM•CE•sin∠MCE}$=$\frac{BM}{CM}$•$\frac{AB}{AC}$①
$\frac{BD}{DC}$=$\frac{BQ}{CP}$•$\frac{AP}{AQ}$=$\frac{BQ}{CP}$•$\frac{AB}{AC}$②,
由①②得:$\frac{BM}{CM}$=$\frac{BQ}{CP}$,
又∠MBA=∠MCA,
∴△MBQ∽△MCP,
∴点M、A、P、Q四点共圆,即点M、A、P、Q、H五点共圆,
又AH为直径,
∴∠AMH=90°.
点评 本题考查了弦切角,掌握塞瓦定理是解题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | k≤-$\frac{4}{3}$或k≥-$\frac{3}{4}$ | B. | k≤$\frac{3}{4}$或k≥$\frac{4}{3}$ | C. | -$\frac{4}{3}$≤k≤-$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
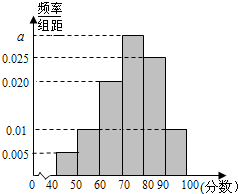 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3x-1 | B. | x+2=0 | C. | $\frac{x}{2}$+$\frac{y}{3}$=1 | D. | 2x-y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com