已知数列{αn}的前n项和为Sn,α1=l,Sn=(2n-1)αn(n∈N*).
(1)证明:数列{αn}是等比数列;
(2)记Tn=n×α1+(n-1)α2+(n-2)α3+…+2×αn-1+1×αn(n∈N*),求L;
(3)证明:当n≥2(n∈N*)时,(1+α1)(1+α2)×…×(1+αn)≤6(1-2αn+1).
(1)证明:∵S
n=(2
n-1)a
n,∴S
n+1=(2
n+1-1)a
n+1,
两式相减可得:a
n+1=(2
n+1-1)a
n+1-(2
n-1)a
n,
∴a
n+1=

a
n,
∵a
1=l,
∴数列{a
n}是以1为首项,

为公比的等比数列;
(2)解:由(1)知,a
n=

∵T
n=n×a
l+(n-1)a
2+(n-2)a
3+…+2×a
n-1+l×a
n,
∴

T
n=n×a
2+(n-1)a
3+(n-2)a
4+…+2×a
n+l×a
n+1,
∴

T
n=n×a
l-(a
2+a
3+…+a
n)-

a
n=n-1+

∴

(3)证明:①当n=2时,左边=(1+α
1)(1+α
2)=3,右边=6(1-2α
n+1)=3,左边=右边,结论成立;
②设n=k(k≥2,k∈N
*)时成立,即(1+α
1)(1+α
2)×…×(1+α
k)≤6(1-2α
k+1),
则n=k+1时,左边=(1+α
1)(1+α
2)×…×(1+α
k)(1+α
k+1)≤6(1-2α
k+1)(1+α
k+1)
下证6(1-2α
k+1)(1+α
k+1)≤6(1-2α
k+2),
即证:-α
k+1-2α
k+12≤-2α
k+2,
即证:

即证:
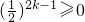
,显然成立.
由①②可知,当n≥2(n∈N
*)时,(1+α
1)(1+α
2)×…×(1+α
n)≤6(1-2α
n+1).
分析:(1)根据数列递推式,再写一式,两式相减,化简可得数列{a
n}是以1为首项,

为公比的等比数列;
(2)求得数列的通项,利用错位相减法可求数列的和;
(3)用数学归纳法证明,关键是第二步设n=k(k≥2,k∈N
*)时成立,即(1+α
1)(1+α
2)×…×(1+α
k)≤6(1-2α
k+1),证明n=k+1时,结论成立,利用分析法进行证明.
点评:本题考查数列递推式,考查等比数列的证明,考查数列的求和,考查数学归纳法证明不等式,确定数列的通项是关键.

 an,
an, 为公比的等比数列;
为公比的等比数列;
 Tn=n×a2+(n-1)a3+(n-2)a4+…+2×an+l×an+1,
Tn=n×a2+(n-1)a3+(n-2)a4+…+2×an+l×an+1, Tn=n×al-(a2+a3+…+an)-
Tn=n×al-(a2+a3+…+an)- an=n-1+
an=n-1+


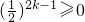 ,显然成立.
,显然成立. 为公比的等比数列;
为公比的等比数列;
