
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
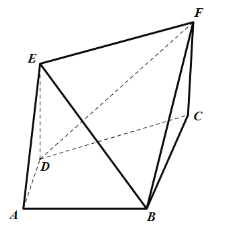
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点P,使得直线
上是否存在点P,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,经过点
,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若![]() ,且
,且![]() 恰为线段
恰为线段![]() 的中点,求证:线段
的中点,求证:线段![]() 的垂直平分线经过定点;
的垂直平分线经过定点;
(2)若![]() ,设
,设![]() 分别为
分别为![]() 的左、右顶点,直线
的左、右顶点,直线![]() 、
、![]() 相交于点
相交于点![]() .当点
.当点![]() 异于
异于![]() 时,
时,![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,图中直棱柱![]() 的底面是菱形,其中
的底面是菱形,其中![]() .又点
.又点![]() 分别在棱
分别在棱![]() 上运动,且满足:
上运动,且满足:![]() ,
,![]() .
.
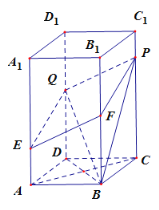
(1)求证:![]() 四点共面,并证明
四点共面,并证明![]() ∥平面
∥平面![]() .
.
(2)是否存在点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?如果存在,求出
?如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菱形![]() 中,
中,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
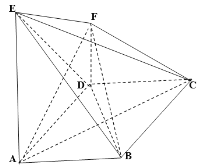
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() 使得直线
使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求
?若存在,求![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线C:![]() 1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若
1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若![]() ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B两地相距100公里,两地政府为提升城市的抗疫能力,决定在A、B之间选址P点建造储备仓库,共享民生物资,当点P在线段AB的中点C时,建造费用为2000万元,若点P在线段AC上(不含点A),则建造费用与P、A之间的距离成反比,若点P在线段CB上(不含点B),则建造费用与P、B之间的距离成反比,现假设P、A之间的距离为x千米![]() ,A地所需该物资每年的运输费用为
,A地所需该物资每年的运输费用为![]() 万元,B地所需该物资每年的运输费用为
万元,B地所需该物资每年的运输费用为![]() 万元,
万元,![]() 表示建造仓库费用,
表示建造仓库费用,![]() 表示两地物资每年的运输总费用(单位:万元).
表示两地物资每年的运输总费用(单位:万元).
![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若规划仓库使用的年限为![]() ,
,![]() ,求
,求![]() 的最小值,并解释其实际意义.
的最小值,并解释其实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com