
(2014•河南一模)已知定义在(0,+∞)上的单调函数f(x),对?x∈(0,+∞),都有f[f(x)﹣log3 x]=4,则函数g(x)=f(x﹣1)﹣f′(x﹣1)﹣3的零点所在区间是( )
A.(1,2) B.(2,3) C.( ,1) D.(0,
,1) D.(0, )
)
B
【解析】
试题分析:由?x∈(0,+∞),都有f[f(x)﹣log3 x]=4,可设f(x)﹣log3 x=c(c为常数),求出g(x)的解析式,并说明g(x)的单调性,计算g(2),g(3),确定符号,由零点存在定理即可得到答案.
【解析】
∵对?x∈(0,+∞),都有f[f(x)﹣log3 x]=4,
∴可设f(x)﹣log3 x=c(c为常数),则f(x)=log3 x+c,
∴f[f(x)﹣log3 x]=f(c)=log3c+c=4,∴c=3,
∴f(x)=log3 x+3,
∴g(x)=f(x﹣1)﹣f′(x﹣1)﹣3=log3(x﹣1)﹣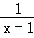 log3e在(1,+∞)上为增函数,
log3e在(1,+∞)上为增函数,
g(2)=﹣log3e<0,g(3)=log32﹣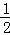 log3e=log3
log3e=log3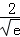 >0,
>0,
由零点存在定理得,函数g(x)的零点所在的区间为(2,3).
故选B.


科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考文科数学试卷(解析版) 题型:解答题
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x米,总费用为y(单位:元).

(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,
并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2014•江西二模)设两个独立事件A,B都不发生的概率为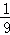 .则A与B都发生的概率值可能为( )
.则A与B都发生的概率值可能为( )
A.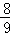 B.
B. C.
C.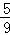 D.
D.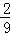
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•河南模拟)设函数f(x)的导函数为f′(x),若对任意x∈R都有f′(x)>f(x)成立,则( )
A.f(ln2014)<2014f(0)
B.f(ln2014)=2014f(0)
C.f(ln2014)>2014f(0)
D.f(ln2014)与2014f(0)的大小关系不确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•江西二模)已知函数f(x)=x2+f′(2)(lnx﹣x),则f′(1)=( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
若平面α与β的法向量分别是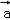 =(1,0,﹣2),
=(1,0,﹣2),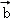 =(﹣1,0,2),则平面α与β的位置关系是( )
=(﹣1,0,2),则平面α与β的位置关系是( )
A.平行 B.垂直 C.相交不垂直 D.无法判断
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,M、N分别是棱DD1、D1C1的中点,则直线OM( )

A.和AC、MN都垂直
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC、MN都不垂直
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.4直线的方向向量练习卷(解析版) 题型:选择题
设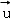 =(2,2,﹣1)是平面α的法向量,
=(2,2,﹣1)是平面α的法向量,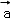 =(﹣3,4,2)是直线l的方向向量,则直线l与α的位置关系是( )
=(﹣3,4,2)是直线l的方向向量,则直线l与α的位置关系是( )
A.l∥α B.l⊥α C.l?α D.l?α或l∥α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com