�⣺��1����Ϊf'��x��=3mx
2+2nx��------��1�֣�
����֪��f'��2��=0������3m+n=0��n=-3m------��2�֣�
��f'��x��=3mx
2-6mx����f'��x����0֪mx��x-2����0��
��m��0ʱ��x��0��x��2��f��x���ļ�����Ϊ��0��2����-----��3�֣�
��m��0ʱ�ã�0��x��2��f��x���ļ�����Ϊ��-�ޣ�0���ͣ�2��+�ޣ���-----��4�֣�
������������m��0ʱ��f��x���ļ�����Ϊ��0��2����
��m��0ʱ��f��x���ļ�����Ϊ��-�ޣ�0���ͣ�2��+�ޣ���-----��5�֣�
��2����

=m��x
12+x
22+x
1x
2-3x
1-3x
2����------------��6�֣�
��
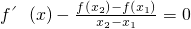
��
�ɻ�Ϊ3x
2-6x-x
12-x
22-x
1x
2+3x
1+3x
2=0����h��x��=3x
2-6x-x
12-x
22-x
1x
2+3x
1+3x
2-------��7�֣�
��h��x
1��=��x
1-x
2����2x
1+x
2-3����h��x
2��=��x
2-x
1����x
1+2x
2-3����
��h��x
1��h��x
2��=-��x
1-x
2��
2��2x
1+x
2-3����x
1+2x
2-3������Ϊ0��x
1��x
2��1�����ԣ�2x
1+x
2-3����0����x
1+2x
2-3����0����h��x
1��h��x
2����0��-----------��8�֣�
��h��x��=0�����䣨x
1��x
2���ڱ��н⣬
������x�ķ���
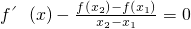
�ڣ�x
1��x
2������ʵ����-----��9�֣�
��3����g��x��=lnx��x�ʣ�a��b����-----------��10�֣�
��g��x����������������ֵ������������������x
0�ʣ�a��b����
ʹ
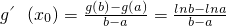
-----------��11�֣�
��Ϊg�䣨x��=

����x�ʣ�a��b����0��a��b��֪g�䣨x���ʣ�

����b-a��0-----��12�֣�
��
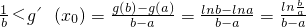

��
��
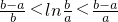
-----��14�֣�
��������1���ȶԺ���f��x���������ָ���f'��2��=0�ɵõ�����m�Ĵ���ʽ���ٽ�m�Ĵ���ʽn���뺯��f��x������ȥn���ɵ�f'��x��=3mx
2-6mx����f'��x����0ʱx��ȡֵ����Ϊ����
��2������

=m��x
12+x
22+x
1x
2-3x
1-3x
2���Ӷ�
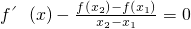
���ɻ�Ϊ3x
2-6x-x
12-x
22-x
1x
2+3x
1+3x
2=0����h��x��=3x
2-6x-x
12-x
22-x
1x
2+3x
1+3x
2��������h��x
1��h��x
2����0�����������ڶ�����h��x��=0�����䣨x
1��x
2���ڱ��н⣬�Ӷ��õ�֤����
��3����g��x��=lnx��x�ʣ�a��b������g��x����������������ֵ������������������x
0�ʣ�a��b����ʹ
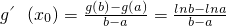
�����ں���g�䣨x��=

�����ʼ���֤�ý����
��������С����Ҫ���鵼�������㡢���õ����о�������ij�����߷��̡�����ʽ�Ľⷨ\����������ֵ�����Ȼ���֪ʶ����������������������黯����ת��˼�룮�����е��⣮

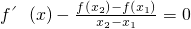 �ڣ�x1��x2������ʵ����
�ڣ�x1��x2������ʵ����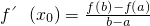 ����������ѧ����ָ�������������������Һ����ȶ���������������ֵ������������������������ֵ����֤����
����������ѧ����ָ�������������������Һ����ȶ���������������ֵ������������������������ֵ����֤����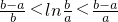 ���ɲ���֤�������������ԺͿɵ��ԣ���
���ɲ���֤�������������ԺͿɵ��ԣ��� =m��x12+x22+x1x2-3x1-3x2����------------��6�֣�
=m��x12+x22+x1x2-3x1-3x2����------------��6�֣�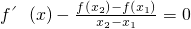 ��
��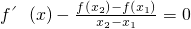 �ڣ�x1��x2������ʵ����-----��9�֣�
�ڣ�x1��x2������ʵ����-----��9�֣�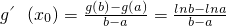 -----------��11�֣�
-----------��11�֣� ����x�ʣ�a��b����0��a��b��֪g�䣨x���ʣ�
����x�ʣ�a��b����0��a��b��֪g�䣨x���ʣ� ����b-a��0-----��12�֣�
����b-a��0-----��12�֣�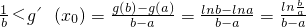
 ��
��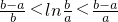 -----��14�֣�
-----��14�֣� =m��x12+x22+x1x2-3x1-3x2���Ӷ�
=m��x12+x22+x1x2-3x1-3x2���Ӷ�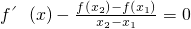 ���ɻ�Ϊ3x2-6x-x12-x22-x1x2+3x1+3x2=0����h��x��=3x2-6x-x12-x22-x1x2+3x1+3x2��������h��x1��h��x2����0�����������ڶ�����h��x��=0�����䣨x1��x2���ڱ��н⣬�Ӷ��õ�֤����
���ɻ�Ϊ3x2-6x-x12-x22-x1x2+3x1+3x2=0����h��x��=3x2-6x-x12-x22-x1x2+3x1+3x2��������h��x1��h��x2����0�����������ڶ�����h��x��=0�����䣨x1��x2���ڱ��н⣬�Ӷ��õ�֤����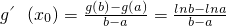 �����ں���g�䣨x��=
�����ں���g�䣨x��= �����ʼ���֤�ý����
�����ʼ���֤�ý����

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�