
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E,F分别在
,点E,F分别在![]() ,
,![]() ,且
,且![]() ,
,![]() .设
.设![]() .
.
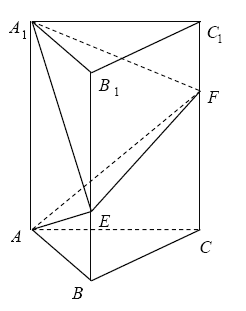
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)当平面![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)60°(2)![]()
【解析】
(1)推导出![]() 平面ABC,
平面ABC,![]() AC,建立分别以AB,AC,
AC,建立分别以AB,AC,![]() 为
为![]() 轴的空间直角坐标系,利用法向量能求出异面直线AE与
轴的空间直角坐标系,利用法向量能求出异面直线AE与![]() 所成角.
所成角.
(2)推导出平面![]() 的法向量和平面
的法向量和平面![]() 的一个法向量,由平面
的一个法向量,由平面![]() 平面
平面![]() ,能求出
,能求出![]() 的值.
的值.
解:因为直三棱柱![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
又因为![]() ,
,
所以建立分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴的空间直角坐标系
轴的空间直角坐标系![]() .
.
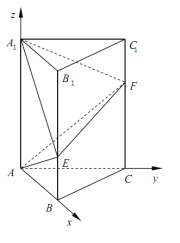
(1)设![]() ,则
,则![]() ,
,![]() ,
,
各点的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,
所以 .
.
所以向量![]() 和
和![]() 所成的角为120°,
所成的角为120°,
所以异面直线![]() 与
与![]() 所成角为60°;
所成角为60°;
(2)因为![]() ,
,![]() ,
,
![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,且
,且![]() .
.
即![]() ,且
,且![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
同理,![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
因为平面![]() 平面
平面![]() ,
,
所以![]() ,
,
![]() ,
,
解得![]() .
.
所以当平面![]() 平面
平面![]() 时,
时,![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:
【题目】已知椭图![]() :
:![]() 的右顶点与抛物线
的右顶点与抛物线![]() :
:![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为
轴的直线截抛物线所得的弦长为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .当直线
.当直线![]() 绕点
绕点![]() 旋转时,直线
旋转时,直线![]() 是否经过一定点?请判断并证明你的结论.
是否经过一定点?请判断并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
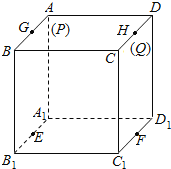
A.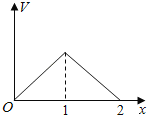 B.
B.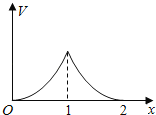
C.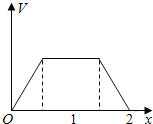 D.
D.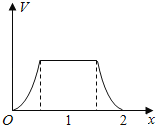
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.
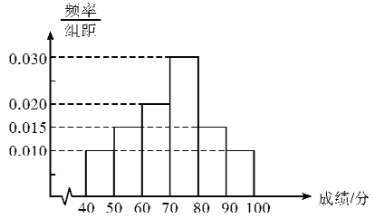
(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个统计案例如下:
①为了探究患慢性支气管炎与吸烟关系,调查了339名50岁以上的人,调查结果如表:
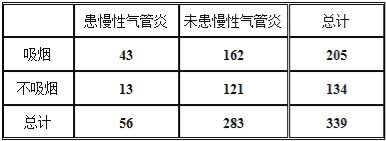
②为了解某地母亲与女儿身高的关系,随机测得10对母女的身高如下表: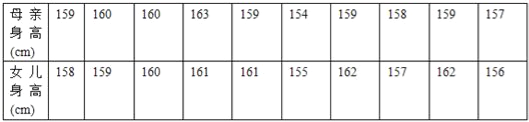
则对这些数据的处理所应用的统计方法是( )
A.①回归分析②取平均值
B.①独立性检验②回归分析
C.①回归分析②独立性检验
D.①独立性检验②取平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障人民群众的身体健康,在预防新型冠状病毒期间,贵阳市市场监督管理局加强了对市场的监管力度,对生产口罩的某工厂利用随机数表对生产的![]() 个口罩进行抽样测试是否合格,先将
个口罩进行抽样测试是否合格,先将![]() 个口罩进行编号,编号分别为
个口罩进行编号,编号分别为![]() ;从中抽取
;从中抽取![]() 个样本,如下提供随机数表的第
个样本,如下提供随机数表的第![]() 行到第
行到第![]() 行:
行:
![]()
![]()
![]()
若从表中第![]() 行第
行第![]() 列开始向右依次读取
列开始向右依次读取![]() 个数据,则得到的第
个数据,则得到的第![]() 个样本编号为( )
个样本编号为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com