
【题目】已知a>0,b∈R,函数f(x)=4ax3﹣2bx﹣a+b.
(1)证明:当0≤x≤1时,
(i)函数f(x)的最大值为|2a﹣b|+a;
(ii)f(x)+|2a﹣b|+a≥0;
(2)若﹣1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.
【答案】
(1)证明:(ⅰ)f′(x)=12a(x2﹣ ![]() )
)
当b≤0时,f′(x)>0,在0≤x≤1上恒成立,此时最大值为:f(1)=|2a﹣b|﹢a;
当b>0时,在0≤x≤1上的正负性不能判断,f'(x)在区间[0,1]先负后可能正,f(x)图象在[0,1]区间内是凹下去的,所以最大值正好取在区间的端点,此时最大值为:f(x)max=max{f(0),f(1)}=|2a﹣b|﹢a;
综上所述:函数在0≤x≤1上的最大值为|2a﹣b|﹢a;
(ⅱ) 要证f(x)+|2a﹣b|+a≥0,即证g(x)=﹣f(x)≤|2a﹣b|﹢a.
亦即证g(x)在0≤x≤1上的最大值小于(或等于)|2a﹣b|﹢a,
∵g(x)=﹣4ax3+2bx+a﹣b,∴令g′(x)=﹣12ax2+2b=0,
当b≤0时, ![]() ;g′(x)<0在0≤x≤1上恒成立,
;g′(x)<0在0≤x≤1上恒成立,
此时g(x)的最大值为:g(0)=a﹣b<3a﹣b=|2a﹣b|﹢a;
当b>0时,g′(x)在0≤x≤1上的正负性不能判断,
∴g(x)max=max{g( ![]() ),g(1)}={
),g(1)}={ ![]() }=
}= 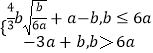
∴g(x)max≤|2a﹣b|﹢a;
综上所述:函数g(x)在0≤x≤1上的最大值小于(或等于)|2a﹣b|﹢a.
即f(x)+|2a﹣b|+a≥0在0≤x≤1上恒成立.
(2)解:由(1)知:函数在0≤x≤1上的最大值为|2a﹣b|﹢a,且函数在0≤x≤1上的最小值比﹣(|2a﹣b|﹢a)要大.
∵﹣1≤f(x)≤1对x∈[0,1]恒成立,
∴|2a﹣b|﹢a≤1.
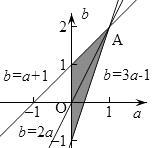
取b为纵轴,a为横轴,则可行域为: ![]() 或
或 ![]() ,目标函数为z=a+b.
,目标函数为z=a+b.
作图如右:
由图易得:a+b的取值范围为(﹣1,3]
【解析】(Ⅰ)(ⅰ)求导函数,再分类讨论:当b≤0时,f′(x)>0在0≤x≤1上恒成立,此时最大值为:f(1)=|2a﹣b|﹢a;当b>0时,在0≤x≤1上的正负性不能判断,此时最大值为:f(x)max=max{f(0),f(1)}=|2a﹣b|﹢a,由此可得结论;(ⅱ) 利用分析法,要证f(x)+|2a﹣b|+a≥0,即证g(x)=﹣f(x)≤|2a﹣b|﹢a.亦即证g(x)在0≤x≤1上的最大值小于(或等于)|2a﹣b|﹢a.(Ⅱ)由(Ⅰ)知:函数在0≤x≤1上的最大值为|2a﹣b|﹢a,且函数在0≤x≤1上的最小值比﹣(|2a﹣b|﹢a)要大.根据﹣1≤f(x)≤1对x∈[0,1]恒成立,可得|2a﹣b|﹢a≤1,从而利用线性规划知识,可求a+b的取值范围.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知函数
中,已知函数![]() 的图像与直线
的图像与直线![]() 相切,其中
相切,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)求实数![]() 的值;
的值;
(2)设函数![]() 在区间
在区间![]() 内有两个极值点.
内有两个极值点.
①求实数![]() 的取值范围;
的取值范围;
②设函数![]() 的极大值和极小值的差为
的极大值和极小值的差为![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=4,AC=BC=3,D为AB的中点 
(1)求点C到平面A1ABB1的距离;
(2)若AB1⊥A1C,求二面角A1﹣CD﹣C1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出此3球所得分数之和.
(1)求X的分布列;
(2)求X的数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等腰梯形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]()
![]() ,将
,将![]() 沿着
沿着![]() 翻折成
翻折成![]() ,使平面
,使平面![]() 平面
平面![]() .
.


(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在点P,使得
上是否存在点P,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ln(x+a)的最小值为0,其中a>0.
(1)求a的值;
(2)若对任意的x∈[0,+∞),有f(x)≤kx2成立,求实数k的最小值;
(3)证明: ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
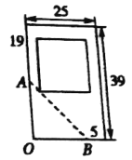
【题目】请你帮忙设计2010年玉树地震灾区小学的新校舍,如图,在学校的东北力有一块地,其中两面是不能动的围墙,在边界![]() 内是不能动的一些体育设施.现准备在此建一栋教学楼,使楼的底面为一矩形,且靠围墙的方向须留有5米宽的空地,问如何设计,才能使教学楼的面积最大?
内是不能动的一些体育设施.现准备在此建一栋教学楼,使楼的底面为一矩形,且靠围墙的方向须留有5米宽的空地,问如何设计,才能使教学楼的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com