
【题目】已知椭圆![]()
![]() 过点
过点![]() ,且离心率
,且离心率![]() .
.
(1)求椭圆的方程;
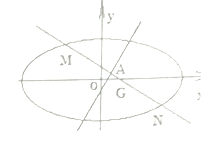
(2)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由离心率得到a,c,b的关系,进一步把椭圆方程用含有c的代数式表示,再结合点![]() 在椭圆上求得c,则椭圆方程可求;(2)设出M,N的坐标,联立直线方程和椭圆方程,由判别式大于0得到
在椭圆上求得c,则椭圆方程可求;(2)设出M,N的坐标,联立直线方程和椭圆方程,由判别式大于0得到![]() ,再结合根与系数关系得到MN中点P的坐标为
,再结合根与系数关系得到MN中点P的坐标为![]() .求出MN的垂直平分线l'方程,由P在l'上,得到
.求出MN的垂直平分线l'方程,由P在l'上,得到![]() ,再结合
,再结合![]() 求得k的取值范围.
求得k的取值范围.
试题解析:(1)离心率![]() ,∴
,∴![]() ,即
,即![]() (1)
(1)
又椭圆过点![]() ,则
,则![]() ,(1)式代入上式,解得:
,(1)式代入上式,解得: ![]() ,
, ![]() ,椭圆方程为
,椭圆方程为![]()
(2)设![]() ,弦
,弦![]() 的中点
的中点![]()
由![]() ,得:
,得: ![]() ,
,
直线![]() 与椭圆交于不同的两点,
与椭圆交于不同的两点,
∴![]() ,即
,即![]() ,(1)
,(1)
由韦达定理得: ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
直线![]() 的斜率为:
的斜率为: 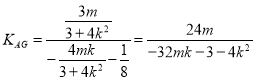 ,
,
由直线![]() 和直线
和直线![]() 垂直可得:
垂直可得: ![]() ,即
,即![]() ,代入(1)式,
,代入(1)式,
可得: 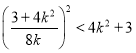 ,即
,即![]() ,则
,则![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,若存在常数T≠0,使得f(x)=Tf(x+T)对任意的x∈R成立,则称函数f(x)是Ω函数. (Ⅰ)判断函数f(x)=x,g(x)=sinπx是否是Ω函数;(只需写出结论)
(Ⅱ)说明:请在(i)、(ii)问中选择一问解答即可,两问都作答的按选择(i)计分
(i)求证:若函数f(x)是Ω函数,且f(x)是偶函数,则f(x)是周期函数;
(ii)求证:若函数f(x)是Ω函数,且f(x)是奇函数,则f(x)是周期函数;
(Ⅲ)求证:当a>1时,函数f(x)=ax一定是Ω函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明与分析
(1)已知a,b为正实数.求证: ![]() +
+ ![]() ≥a+b;
≥a+b;
(2)某题字迹有污损,内容是“已知|x|≤1, ![]() ,用分析法证明|x+y|≤|1+xy|”.试分析污损部分的文字内容是什么?并说明理由.
,用分析法证明|x+y|≤|1+xy|”.试分析污损部分的文字内容是什么?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一点在直线上从时刻t=0(s)开始以速度v(t)=t2﹣4t+3(m/s)运动,求:
(1)在t=4s时的位置;
(2)在t=4s的运动路程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
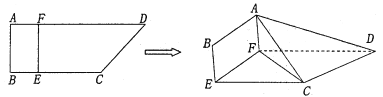
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
(1)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)求三棱锥![]() 的体积的最大值,并求出此时点
的体积的最大值,并求出此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com