
【题目】证明与分析
(1)已知a,b为正实数.求证: ![]() +
+ ![]() ≥a+b;
≥a+b;
(2)某题字迹有污损,内容是“已知|x|≤1, ![]() ,用分析法证明|x+y|≤|1+xy|”.试分析污损部分的文字内容是什么?并说明理由.
,用分析法证明|x+y|≤|1+xy|”.试分析污损部分的文字内容是什么?并说明理由.
【答案】
(1)证明:∵a>0,b>0,
∴(a+b)( ![]() )=a2+b2+
)=a2+b2+ ![]() ≥a2+b2+2ab=(a+b)2.
≥a2+b2+2ab=(a+b)2.
∴ ![]() ≥a+b,当且仅当a=b时等号成立.
≥a+b,当且仅当a=b时等号成立.
(2)解:污损部分的文字内容为“|y|≤1”.理由如下:
要证:|x+y|≤|1+xy|,只需证:(x+y)2≤(1+xy)2,即证:x2+y2≤1+x2y2,
只需证:(x2﹣1)(1﹣y2)≤0,
∵|x|≤1,故只需证:1﹣y2≥0即可.
∴估计污损部分的文字内容为“|y|≤1”.
【解析】(1)不等式两边同乘(a+b),使用基本不等式即可得出结论;(2)将结论两边平方即可得出(x2﹣1)(1﹣y2)≤0,故只需1﹣y2≥0即可.
【考点精析】本题主要考查了不等式的证明的相关知识点,需要掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能正确解答此题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
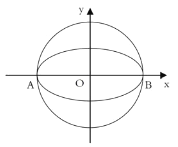
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,与圆
,与圆![]() 的另一个交点为
的另一个交点为![]() .
.
(ⅰ)当![]() 时,求直线
时,求直线![]() 的斜率;
的斜率;
(ⅱ)是否存在直线![]() ,使
,使![]() ?若存在,求出直线
?若存在,求出直线![]() 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: 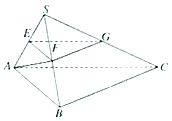
(1)平面EFG∥平面ABC;
(2)BC⊥平面SAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)证明:不论m取什么数,直线l与圆C恒交于两点;
(2)求直线l被圆C截得的线段的最短长度,并求此时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形内切圆的半径是高的 ![]() ,把这个结论推广到正四面体,类似的结论正确的是( )
,把这个结论推广到正四面体,类似的结论正确的是( )
A.正四面体的内切球的半径是高的 ![]()
B.正四面体的内切球的半径是高的 ![]()
C.正四面体的内切球的半径是高的 ![]()
D.正四面体的内切球的半径是高的 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx﹣ ![]() )(A>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为
)(A>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为 ![]() . (Ⅰ)求函数f(x)的最小正周期及解析式;
. (Ⅰ)求函数f(x)的最小正周期及解析式;
(Ⅱ)求函数f(x)的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的图象过点(﹣1,2),且在点(﹣1,f(﹣1))处的切线与直线x﹣5y+1=0垂直.
的图象过点(﹣1,2),且在点(﹣1,f(﹣1))处的切线与直线x﹣5y+1=0垂直.
(1)求实数b,c的值;
(2)求f(x)在[﹣1,e](e为自然对数的底数)上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com