
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
【答案】(1)![]() .(2)
.(2)![]()
【解析】试题分析:(1)求出抛物线的焦点坐标,结合题意列关于p的等式求p,则抛物线方程可求;
(2)由(1)求出M的坐标,设出直线DE的方程![]() ,联立直线方程和抛物线方程,化为关于y的一元二次方程后D,E两点纵坐标的和与积,利用
,联立直线方程和抛物线方程,化为关于y的一元二次方程后D,E两点纵坐标的和与积,利用![]() 得到t与m的关系,进一步得到DE方程,由直线系方程可得直线DE所过定点.
得到t与m的关系,进一步得到DE方程,由直线系方程可得直线DE所过定点.
试题解析:
(1)由题意设抛物线方程为![]() ,
,
其准线方程为![]() ,
,
∵![]() 到焦点的距离等于
到焦点的距离等于![]() 到其准线的距离,
到其准线的距离,
∴![]() ,∴
,∴![]() .
.
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)可得点![]() ,可得直线
,可得直线![]() 的斜率不为0,
的斜率不为0,
设直线![]() 的方程为:
的方程为: ![]() ,
,
联立![]() ,得
,得![]() ,
,
则![]() ①.
①.
设![]() ,则
,则![]() .
.
∵![]()
![]()
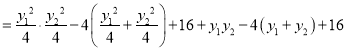
![]()
![]()
即![]() ,得:
,得: ![]() ,
,
∴![]() ,即
,即![]() 或
或![]() ,
,
代人①式检验均满足![]() ,
,
∴直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.
∴直线过定点![]() (定点
(定点![]() 不满足题意,故舍去).
不满足题意,故舍去).
点睛:抛物线的定义是解决抛物线问题的基础,它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化.如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线定义就能解决问题.因此,涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离,这样就可以使问题简单化.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且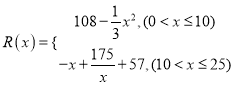 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明与分析
(1)已知a,b为正实数.求证: ![]() +
+ ![]() ≥a+b;
≥a+b;
(2)某题字迹有污损,内容是“已知|x|≤1, ![]() ,用分析法证明|x+y|≤|1+xy|”.试分析污损部分的文字内容是什么?并说明理由.
,用分析法证明|x+y|≤|1+xy|”.试分析污损部分的文字内容是什么?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2x+2 ![]() sinxcosx+a,且当
sinxcosx+a,且当 ![]() 时,f(x)的最小值为2.
时,f(x)的最小值为2.
(1)求a的值,并求f(x)的单调增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ![]() ,再把所得图象向右平移
,再把所得图象向右平移 ![]() 个单位,得到函数y=g(x),求方程g(x)=2在区间
个单位,得到函数y=g(x),求方程g(x)=2在区间 ![]() 上的所有根之和.
上的所有根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|3≤3x≤27}, ![]() .
.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com