
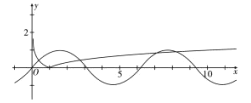
【题目】函数![]() 有4个零点,其图象如下图,和图象吻合的函数解析式是( )
有4个零点,其图象如下图,和图象吻合的函数解析式是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】根据图像及零点的意义可知,图像为两个函数的交点,分别为![]() 和
和![]() .
.
故![]() .
.
故选D.
得解:本函数图象的交点、函数的零点、方程的根往往是“知一求二”,解答时要先判断哪个好求解就转化为哪个,判断函数![]() 零点个数的常用方法:(1) 直接法: 令
零点个数的常用方法:(1) 直接法: 令![]() 则方程实根的个数就是函数零点的个;(2) 零点存在性定理法:判断函数在区间
则方程实根的个数就是函数零点的个;(2) 零点存在性定理法:判断函数在区间![]() 上是连续不断的曲线,且
上是连续不断的曲线,且![]() 再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数;(3) 数形结合法:转化为两个函数的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,在一个区间上单调的函数在该区间内至多只有一个零点,在确定函数零点的唯一性时往往要利用函数的单调性,确定函数零点所在区间主要利用函数零点存在定理,有时可结合函数的图象辅助解题.
再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数;(3) 数形结合法:转化为两个函数的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,在一个区间上单调的函数在该区间内至多只有一个零点,在确定函数零点的唯一性时往往要利用函数的单调性,确定函数零点所在区间主要利用函数零点存在定理,有时可结合函数的图象辅助解题.


科目:高中数学 来源: 题型:
【题目】下列命题:①函数f(x)=sin2x一cos2x的最小正周期是![]() ;
;
②在等比数列〔![]() }中,若
}中,若![]() ,则a3=士2;
,则a3=士2;
③设函数f(x)=![]() ,若
,若![]() 有意义,则
有意义,则![]()
④平面四边形ABCD中, ![]() ,则四边形ABCD是
,则四边形ABCD是
菱形. 其中所有的真命题是:( )
A. ①②④ B. ①④ C. ③④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为 ![]() ,则实数a的值为( )
,则实数a的值为( )
A.![]()
B.![]() 或
或 ![]()
C.![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
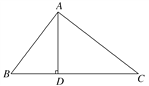
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:
①∠B+∠DAC=90°,
②∠B=∠DAC,
③![]() ,
,
④AB2=BD·BC.
其中一定能够判定△ABC是直角三角形的共有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)证明:不论m取什么数,直线l与圆C恒交于两点;
(2)求直线l被圆C截得的线段的最短长度,并求此时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx﹣ax(a> ![]() ),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于 .
),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
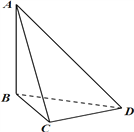
【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,则三棱锥
,则三棱锥![]() 的外接球的球面面积为__________.
的外接球的球面面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com