
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 根据cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=cos<$\overrightarrow{OA}$,$\overrightarrow{OC}$>和|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{OA}$•$\overrightarrow{OC}$.故而$\overrightarrow{OA}$•$\overrightarrow{BC}$=$\overrightarrow{OA}$•($\overrightarrow{OC}-\overrightarrow{OB}$)=0,得出$\overrightarrow{OA}⊥\overrightarrow{BC}$.
解答 解:∵cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=cos<$\overrightarrow{OA}$,$\overrightarrow{OC}$>,∴$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=$\frac{\overrightarrow{OA}•\overrightarrow{OC}}{|\overrightarrow{OA}|•|\overrightarrow{OC}|}$,
∵|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{OA}$•$\overrightarrow{OC}$,∴$\overrightarrow{OA}$•$\overrightarrow{BC}$=$\overrightarrow{OA}$•($\overrightarrow{OC}-\overrightarrow{OB}$)=0,∴$\overrightarrow{OA}⊥\overrightarrow{BC}$.
∴sin<$\overrightarrow{OA}$,$\overrightarrow{BC}$>=sin$\frac{π}{2}$=1.
故选:A.
点评 本题考查了空间向量的数量积运算,夹角公式,向量垂直与数量积的关系,属于中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$] | B. | (-∞,4] | C. | [$\frac{3}{2}$,2] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1,1) | B. | (-$\frac{1}{2}$,-$\frac{3}{2}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$,-1) | D. | ($\sqrt{2}$,-3,-2$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
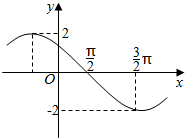 已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则f(x)解析式是( )
已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则f(x)解析式是( )| A. | f(x)=2sin($\frac{1}{2}$x-$\frac{π}{4}$) | B. | f(x)=2sin($\frac{1}{2}$x+$\frac{3π}{4}$) | C. | f(x)=2sin(2x-$\frac{π}{4}$) | D. | f(x)=2sin(2x+$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com