
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在经过点![]() 的直线
的直线![]() ,它与椭圆
,它与椭圆![]() 相交于
相交于![]() 两个不同点,且满足
两个不同点,且满足![]() 为坐标原点)关系的点
为坐标原点)关系的点![]() 也在椭圆
也在椭圆![]() 上,如果存在,求出直线
上,如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
【答案】(1) ![]() ; (2)存在,
; (2)存在,![]()
【解析】
(1)根据椭圆离心率为![]() ,得
,得![]() ,将点
,将点![]() 代入椭圆方程,即可求解;
代入椭圆方程,即可求解;
(2)分类讨论当斜率不存在时和斜率存在时直线是否满足题意,联立直线和椭圆的方程,结合韦达定理用点的坐标代入运算即可求解.
解:(1)由椭圆的离心率为![]() ,得
,得![]() ,再由点
,再由点![]() 在椭圆上,得
在椭圆上,得
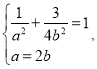 解得
解得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)因为点![]() 在椭圆内部,经过点
在椭圆内部,经过点![]() 的直线
的直线![]() 与椭圆恒有两个交点,假设直线
与椭圆恒有两个交点,假设直线![]() 存在,
存在,
当斜率不存在时,经过点![]() 的直线
的直线![]() 的方程
的方程![]() ,与椭圆交点坐标为
,与椭圆交点坐标为
![]() 或
或![]() ,
,
当![]() 时,
时,
![]() ,
,
所以![]() ,
,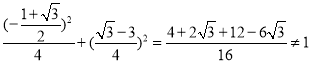 ,
,
点![]() 不在椭圆上;
不在椭圆上;
当![]() 时,
时,
![]() ,
,
同上可得:![]() 不在椭圆上,
不在椭圆上,
所以直线![]() 不合题意;
不合题意;
当斜率存在时:设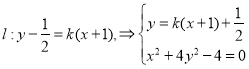
![]() ,
,
设![]() ,由韦达定理得
,由韦达定理得
![]()
![]()
因为点![]() 在椭圆
在椭圆![]() 上,因此得
上,因此得![]() ,
,
由![]() ,
,
由于点![]() 也在椭圆
也在椭圆![]() 上,则
上,则
![]() ,整理得,
,整理得,
![]() ,即
,即![]()
所以![]()
因此直线![]() 的方程为
的方程为![]()


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() x2=1(a>1)与抛物线C2:x2=4y有相同焦点F1.
x2=1(a>1)与抛物线C2:x2=4y有相同焦点F1.
(1)求椭圆C1的标准方程;
(2)已知直线l1过椭圆C1的另一焦点F2,且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
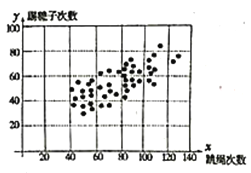
【题目】为庆祝“三八妇女节”,![]() 校组织该校48名女教职工参加跳绳与踢毽子两项健身活动.在规则下,成绩统计如图,
校组织该校48名女教职工参加跳绳与踢毽子两项健身活动.在规则下,成绩统计如图,![]() 代表跳绳的次数,
代表跳绳的次数,![]() 代表踢毽子的次数,并设置奖励标准:
代表踢毽子的次数,并设置奖励标准:![]() 且
且![]() 为一等奖,每人奖励300元;
为一等奖,每人奖励300元;![]() 或
或![]() 为三等奖,每人奖励100元;其余皆为二等奖,每人奖励200元;
为三等奖,每人奖励100元;其余皆为二等奖,每人奖励200元;
(1)试估计该校女教职工获得奖金的平均数;
(2)从该校跳绳成绩![]() 的女教职工中随机抽取两人,若对拿到单项最高成绩者额外奖励每人100元,记这两人的奖金之和为
的女教职工中随机抽取两人,若对拿到单项最高成绩者额外奖励每人100元,记这两人的奖金之和为![]() ,求
,求![]() .
.
(3)鉴于此项活动健康有趣,导向积极,易于操作,引得其他学校竞相效仿,相继举行此项活动(并设立同样的奖励标准).若以样本估计总体,从参加此项活动的女教职工(人数很多)中随机抽取两人,记这两人所获奖金之和为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 的数据作了初步整理,得到下面的表格:
的数据作了初步整理,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
(1)用年广告费![]() 作解释变量,年销售额
作解释变量,年销售额![]() 作预报变量,在所给坐标系中作出这些数据的散点图,并判断
作预报变量,在所给坐标系中作出这些数据的散点图,并判断![]() 与
与![]() 哪一个更适合作为年销售额
哪一个更适合作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型(给出判断即可,不必说明理由).
的回归方程类型(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() .根据(2)的结果,计算年广告费
.根据(2)的结果,计算年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据
约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为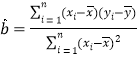 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 、
、![]() (
(![]() ),
),![]() 与
与![]() 恰有一个公共点
恰有一个公共点![]() ,
,![]() 与
与![]() 恰有一个公共点
恰有一个公共点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)当![]() 时,求点
时,求点![]() 到
到![]() 准线的距离;
准线的距离;
(2)当![]() 与
与![]() 不垂直时,求
不垂直时,求![]() 的取值范围;
的取值范围;
(3)设![]() 是平面上一点,满足
是平面上一点,满足![]() 且
且![]() ,求
,求![]() 和
和![]() 的夹角大小.
的夹角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别是
的两个焦点分别是![]() ,
, ![]() ,且点
,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于异于
相交于异于![]() 的不同两点
的不同两点![]() ,
, ![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:
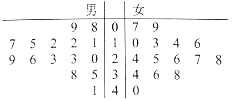
若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人?
(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人,参加读书日宣传活动.
(i)共有多少种不同的抽取方法?
(ii)求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com