
【题目】某企业为了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 的数据作了初步整理,得到下面的表格:
的数据作了初步整理,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
(1)用年广告费![]() 作解释变量,年销售额
作解释变量,年销售额![]() 作预报变量,在所给坐标系中作出这些数据的散点图,并判断
作预报变量,在所给坐标系中作出这些数据的散点图,并判断![]() 与
与![]() 哪一个更适合作为年销售额
哪一个更适合作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型(给出判断即可,不必说明理由).
的回归方程类型(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() .根据(2)的结果,计算年广告费
.根据(2)的结果,计算年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据
约为何值时(小数点后保留两位),年利润的预报值最大.附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为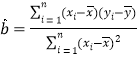 ,
,![]() .
.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】给出下列三种说法:
①命题p:x0∈R,tan x0=1,命题q:x∈R,x2-x+1>0,则命题“p∧(![]() )”是假命题.
)”是假命题.
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是![]() =-3.
=-3.
③命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”.
其中所有正确说法的序号为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数![]() 的图象,需对函数
的图象,需对函数![]() 的图象所作的变换可以为( )
的图象所作的变换可以为( )
A. 先将图象上所有点的横坐标压缩为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位
个单位
B. 先向左平移![]() 个单位,再将图象上所有点的横坐标压缩为原来的
个单位,再将图象上所有点的横坐标压缩为原来的![]() ,纵坐标不变
,纵坐标不变
C. 先向左平移![]() 个单位,再将图象上所有点的横坐标压缩为原来的
个单位,再将图象上所有点的横坐标压缩为原来的![]() ,纵坐标不变
,纵坐标不变
D. 先向右平移![]() 个单位,再将图象上所有点的横坐标伸长为原来的3倍,纵坐标不变
个单位,再将图象上所有点的横坐标伸长为原来的3倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的左焦点,离心率为
的左焦点,离心率为![]() ,直线
,直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中点,
的中点,![]() 是椭圆
是椭圆![]() 上一点,求
上一点,求![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四棱锥![]() 中,
中,![]() 底面
底面![]() ,面
,面![]() 是直角梯形,
是直角梯形,![]() 为侧棱
为侧棱![]() 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
(1)证明:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点![]() ,并求
,并求![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.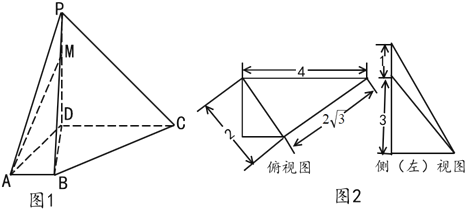
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在经过点![]() 的直线
的直线![]() ,它与椭圆
,它与椭圆![]() 相交于
相交于![]() 两个不同点,且满足
两个不同点,且满足![]() 为坐标原点)关系的点
为坐标原点)关系的点![]() 也在椭圆
也在椭圆![]() 上,如果存在,求出直线
上,如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: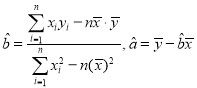
查看答案和解析>>
科目:高中数学 来源: 题型:
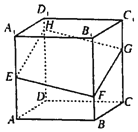
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,作平面
,作平面![]() 与底面不平行
与底面不平行![]() 与棱
与棱![]() ,
,![]() ,
,![]() ,
,![]() 分别交于E,F,G,H,记EA,FB,GC,HD分别为
分别交于E,F,G,H,记EA,FB,GC,HD分别为![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则多面体EFGHABCD的体积为
,则多面体EFGHABCD的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com