练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义域为的函数是奇函数.

    (1) 求实数的值；

    (2) 判断并用定义证明该函数在定义域上的单调性；

    (3) 若方程在内有解，求实数的取值范围．

    【答案】（1）1；（2）见解析；（3）[-1，3）.

    【解析】

    (1)根据解得，再利用奇偶性的定义验证，即可求得实数的值；(2)先对分离常数后，判断出为递减函数，再利用单调性的定义作差证明即可；(3)先用函数的奇函数性质，再用减函数性质变形，然后分离参数可得，在内有解，令，只要.

    （1）依题意得，，故，此时，

    对任意均有，

    所以是奇函数，所以.

    （2）在上是减函数，证明如下：任取，则

    所以该函数在定义域上是减函数．

    （3）由函数为奇函数知，

    ，

    又函数是单调递减函数，从而，

    即方程在内有解，

    令，只要，

    ， 且，∴

    ∴当时，原方程在内有解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，F1、F2分别是双曲线 =1（a＞0，b＞0）的两个焦点，以坐标原点O为圆心，|OF1|为半径的圆与该双曲线左支交于A、B两点，若△F2AB是等边三角形，则双曲线的离心率为 （ ）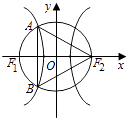

    A.
    B.2
    C. ﹣1
    D.1+

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.

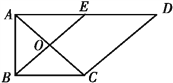
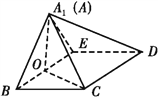
    　　　　　图1　　　　　　　　　　　　　图2

    (1)证明:CD⊥平面A1OC;

    (2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是定义域为的奇函数，且.

    （1）求的解析式；

    （2）证明在区间上是增函数；

    （3）求不等式的解集.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24，单位：时)的函数，记作：．下表是某日各时的浪高数据.

    t(时)

    0

    3

    6

    9

    12

    15

    18

    21

    24

    y(米)

    1.5

    1.0

    0.5

    1.0

    1.5

    1.0

    0.5

    0.99

    1.5

    (1)根据以上数据，求函数y＝f(t)的函数表达式；

    (2)依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据(1)的结论，判断一天内的上午8：00时至晚上20：00时之间，有多少时间可供冲浪者进行运动？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求f（x）的定义域和值域；

    （2）判断f（x）的奇偶性与单调性；

    （3）解关于x的不等式f（x2﹣2x+2）+f（﹣5）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某服装厂生产一种服装，每件服装成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，规定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低元，根据市场调查，销售商一次订购不会超过600件.

    （1）设一次订购件，服装的实际出厂单价为元，写出函数的表达式；

    （2）当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的一系列对应值如下表：

    （1）根据表格提供的数据求函数的一个解析式；

    （2）根据（1）的结果，若函数周期为，当时，方程 恰有两个不同的解，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆(x－3) 2＋(y＋4) 2＝1关于直线x＋y＝0对称的圆的方程是(　　)

    A. (x＋3)2＋(y－4)2＝1

    B. (x－4)2＋(y＋3)2＝1

    C. (x＋4)2＋(y－3)2＝1

    D. (x－3)2＋(y－4)2＝1

    查看答案和解析>>

    同步练习册答案