解答:
解:(1)∵函数
f(x)=lnx-ax+-1(a>0),
所以f′(x)=
(x>0),
令h(x)=ax
2-x+1-a(x>0)
当a≠0时,由f′(x)=0,即ax
2-x+1-a=0,解得x
1=1,x
2=
-1.
当a=
时x
1=x
2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;
当0<a<
时,
-1>1>0,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;
x∈(1,
-1)时,h(x)<0,f′(x)>0,函数f(x)单调递增;
x∈(
-1,+∞)时,h(x)>0,f′(x)<0,函数f(x)单调递减.
当
<a<1时,0<
-1<1,x∈(0,
-1)时h(x)>0,f′(x)<0,函数f(x)单调递减;
x∈(
-1,1)时,h(x)<0,f′(x)>0,函数f(x)单调递增;
x∈(1,+∞)时,h(x)>0,f′(x)<0,函数f(x)单调递减
综上所述:当0<a<
时,函数f(x)在(0,1)、(
-1,+∞)单调递减,(1,
-1)单调递增;
当a=
时x
1=x
2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;
当
<a<1时,函数f(x)在(0,
-1)单调递减,(
-1,1)单调递增,(1,+∞)单调递减.
(2)当
a=时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,
所以对任意x
1∈(0,2),有f(x
1)≥f(1)=-
,
又已知存在x
2∈[1,2],使f(x
1)≥g(x
2),
所以-
≥g(x
2),x
2∈[1,2],(※)
又g(x)=(x-b)
2+4-b
2,x∈[1,2]
当b<1时,g(x)
min=g(1)=5-2b>0与(※)矛盾;
当b∈[1,2]时,g(x)
min=g(b)=4-b
2≥0也与(※)矛盾;
当b>2时,g(x)
min=g(2)=8-4b≤-
,所以b≥
.
综上,实数b的取值范围是[
,+∞).



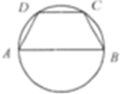 如图,已知AB=2c(2c为常数且c>0).以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若椭圆以A、B为焦点.且过C、D两点,则当梯形ABCD的面积最大时,椭圆的离心率为
如图,已知AB=2c(2c为常数且c>0).以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若椭圆以A、B为焦点.且过C、D两点,则当梯形ABCD的面积最大时,椭圆的离心率为