
| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
分析 根据向量数量积公式以及模长公式分别分析选项即可.
解答 解:因为两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,所以$\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为|$\overrightarrow{{e}_{1}}$|cosθ=cosθ;故A正确;
$\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$=|$\overrightarrow{{e}_{1}^{2}}$|=|$\overrightarrow{{e}_{2}^{2}}$|=1;故B正确;
($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$)=$\overrightarrow{{e}_{1}^{2}}$-$\overrightarrow{{e}_{2}^{2}}$=0;故C正确;
|$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=|$\overrightarrow{{e}_{1}}$|•|$\overrightarrow{{e}_{2}}$||cosθ|=|cosθ|≠1;故D错误;
故选D.
点评 本题考查了单位向量的性质;主要利用了平面向量的数量积公式.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
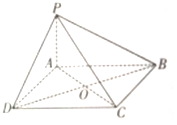 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com