
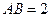 ,
,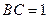 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为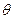 ,且
,且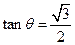 ,
, 平面ABC.
平面ABC. 平面ADE;
平面ADE;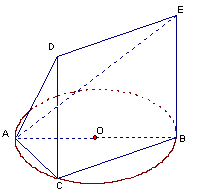
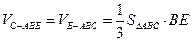
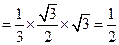
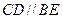
 平面ABC ∴
平面ABC ∴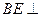 平面ABC
平面ABC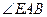 为AE与平面ABC所成的角,
为AE与平面ABC所成的角,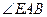 =
=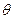 --------------------2分
--------------------2分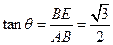 ,
,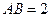 得
得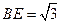 ------------3分
------------3分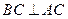
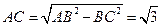
 ∴
∴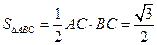 ……………………………………………………4分
……………………………………………………4分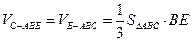
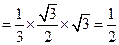 ……………………………………5分
……………………………………5分 平面ABC ,
平面ABC ,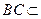 平面ABC ∴
平面ABC ∴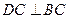 .…………………6分
.…………………6分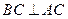 且
且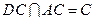 ∴
∴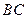
 平面ADC.
平面ADC. 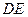
 平面ADC …………………………………………8分
平面ADC …………………………………………8分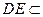 平面ADE ∴平面ACD
平面ADE ∴平面ACD 平面
平面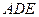 …………………………9分
…………………………9分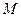 ,使得MO∥平面
,使得MO∥平面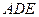 ,该点
,该点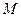 为
为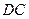 的中点.…… 10分
的中点.…… 10分 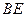 的中点
的中点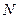 ,连MO、MN、NO,
,连MO、MN、NO,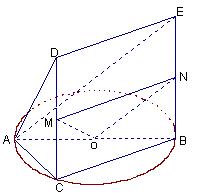
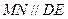 …………………………………………………………11分
…………………………………………………………11分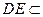 平面ADE,
平面ADE,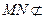 平面ADE,
平面ADE,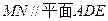 …………………………………………………………12分
…………………………………………………………12分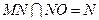 ,∴平面MNO//平面ADE.……………………………………13分
,∴平面MNO//平面ADE.……………………………………13分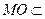 平面MNO,∴MO//平面ADE.……………… 14分(其它证法请参照给分)
平面MNO,∴MO//平面ADE.……………… 14分(其它证法请参照给分)

科目:高中数学 来源:不详 题型:解答题
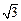 ,∠ACB=90°。
,∠ACB=90°。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
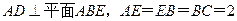 ,F为CE上的点,且BF
,F为CE上的点,且BF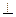 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G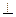 平面BCE
平面BCE查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
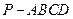 中,
中,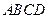 是矩形,三角形PAD为等腰直角三角形,
是矩形,三角形PAD为等腰直角三角形,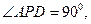 面
面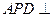 面
面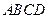 ,
,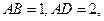
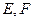 分别为
分别为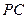 和
和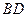 的中点。
的中点。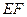 ∥平面
∥平面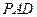 ;
;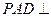 平面
平面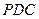 ;
;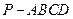 的体积。
的体积。 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
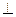 面ABC,BC
面ABC,BC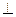 AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。 P,使得CP
P,使得CP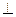 面BDC1,试求AA1的长及点P的位置。
面BDC1,试求AA1的长及点P的位置。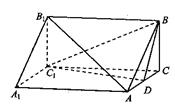
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
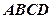 ,
,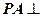 平面
平面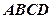 ,
,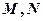 分别是
分别是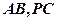 的中点,
的中点,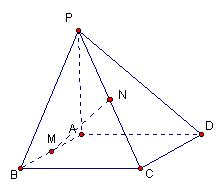
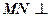 直线
直线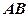 ,
,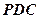 与平面
与平面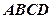 所成的锐二面角为
所成的锐二面角为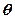 ,能否确定
,能否确定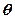 使直线
使直线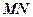 是异面直线
是异面直线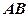 与
与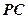 的公垂线.若能确定,求出
的公垂线.若能确定,求出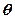 的值;若不能确定,说明理由。
的值;若不能确定,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
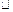 ABC中,两直角边分别为a,b,斜边上的高为h,则得
ABC中,两直角边分别为a,b,斜边上的高为h,则得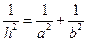 ”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com