
【题目】已知抛物线![]() :
:![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为抛物线
为抛物线![]() 的焦点,若
的焦点,若![]() ,则
,则![]() 的中点的横坐标为( )
的中点的横坐标为( )
A. ![]() B. 3C. 5D. 6
B. 3C. 5D. 6
【答案】A
【解析】
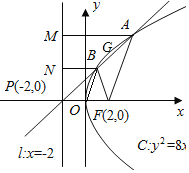
据题意,设AB的中点为G,根据直线方程可知直线恒过定点,据此过A、B分别作AM⊥l于M,BN⊥l于N,根据|FA|=2|FB|,推断出|AM|=2|BN|,点B为AP的中点、连接OB,进而分析可得|OB|=|BF|,进而求得点B的横坐标,则点B的坐标可得,又由B为P、A的中点,可得A的横坐标,进而由中点坐标公式分析可得答案.
根据题意,设AB的中点为G,
抛物线C:y2=8x的准线为l:x=﹣2,焦点为(2,0),
直线y=k(x+2)恒过定点P(﹣2,0)
如图过A、B分别作AM⊥l于M,BN⊥l于N,
由|FA|=2|FB|,则|AM|=2|BN|,
点B为AP的中点、连接OB,则|OB|![]() |AF|,
|AF|,
又由|FA|=2|FB|,则|OB|=|BF|,点B的横坐标为1,
B为P、A的中点,则A的横坐标为4,
故AB的中点G的横坐标为![]() ;
;
故选:A.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 在圆内,在过点P所作的圆的所有弦中,弦长最小值为
在圆内,在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
(1)求实数a的值;
(2)若点M为圆外的动点,过点M向圆C所作的两条切线始终互相垂直,求点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“爱国,是人世间最深层、最持久的情感,是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中,爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造,根据市场调研与模拟,得到科技改造投入![]() (亿元)与科技改造直接收益
(亿元)与科技改造直接收益![]() (亿元)的数据统计如下:
(亿元)的数据统计如下:
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当![]() 时,建立了
时,建立了![]() 与
与![]() 的两个回归模型:模型①:
的两个回归模型:模型①:![]() ;模型②:
;模型②:![]() ;当
;当![]() 时,确定
时,确定![]() 与
与![]() 满足的线性回归方程为:
满足的线性回归方程为:![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①、②的相关指数
时模型①、②的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
(附:刻画回归效果的相关指数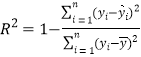 ,
,![]() .)
.)
(2)为鼓励科技创新,当科技改造的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较科技改造投入17亿元与20亿元时公司实际收益的大小;
(附:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式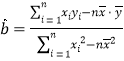
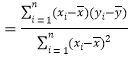 ;
;![]() )
)
(3)科技改造后,“东方红”款汽车发动机的热效![]() 大幅提高,
大幅提高,![]() 服从正态分布
服从正态分布![]() ,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过
,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过![]() ,不予奖励;若发动机的热效率超过
,不予奖励;若发动机的热效率超过![]() 但不超过
但不超过![]() ,每台发动机奖励2万元;若发动机的热效率超过
,每台发动机奖励2万元;若发动机的热效率超过![]() ,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
(附:随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆柱![]() 中,点
中,点![]() 、
、![]() 分别为上、下底面的圆心,平面
分别为上、下底面的圆心,平面![]() 是轴截面,点
是轴截面,点![]() 在上底面圆周上(异于
在上底面圆周上(异于![]() 、
、![]() ),点
),点![]() 为下底面圆弧
为下底面圆弧![]() 的中点,点
的中点,点![]() 与点
与点![]() 在平面
在平面![]() 的同侧,圆柱
的同侧,圆柱![]() 的底面半径为1,高为2.
的底面半径为1,高为2.
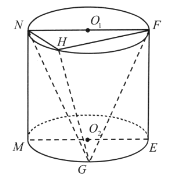
(1)若平面![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)若直线![]() 平面
平面![]() ,求
,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为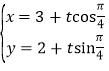 (其中
(其中![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com