Question

【题目】“爱国，是人世间最深层、最持久的情感，是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中，爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造，根据市场调研与模拟，得到科技改造投入（亿元）与科技改造直接收益（亿元）的数据统计如下：

	2	3	4	6	8	10	13	21	22	23	24	25
	13	22	31	42	50	56	58	68.5	68	67.5	66	66

当时，建立了与的两个回归模型：模型①：；模型②：；当时，确定与满足的线性回归方程为：.

（1）根据下列表格中的数据，比较当时模型①、②的相关指数，并选择拟合精度更高、更可靠的模型，预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.

回归模型	模型①	模型②
回归方程
	182.4	79.2

（附：刻画回归效果的相关指数，.）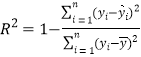

（2）为鼓励科技创新，当科技改造的投入不少于20亿元时，国家给予公司补贴收益10亿元，以回归方程为预测依据，比较科技改造投入17亿元与20亿元时公司实际收益的大小；

（附：用最小二乘法求线性回归方程的系数公式 ；）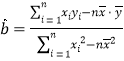

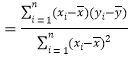（3）科技改造后，“东方红”款汽车发动机的热效大幅提高，服从正态分布，公司对科技改造团队的奖励方案如下：若发动机的热效率不超过，不予奖励；若发动机的热效率超过但不超过，每台发动机奖励2万元；若发动机的热效率超过，每台发动机奖励5万元.求每台发动机获得奖励的数学期望.

（附：随机变量服从正态分布，则，.）

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）由表格中的数据，结合刻画回归效果的相关指数，可得结论；（2）求得样本，可得当x＞17亿元时，y与x满足的线性回归方程，令x＝20，可得所求大小；（3）由正态分布的计算公式，以及数学期望公式，可得所求值．

（1）由表格中的数据，有，即，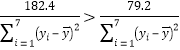

所以模型①的小于模型②，说明回归模型②刻画的拟合效果更好.

所以当亿元时，科技改造直接收益的预测值为

（亿元）.

（2）由已知可得：，所以.

，所以.

所以.

所以当亿元时，与满足的线性回归方程为：.

所以当亿元时，科技改造直接收益的预测值.

所以当亿元时，实际收益的预测值为亿元亿元.

所以技改造投入20亿元时，公司的实际收益的更大.

（3）因为，

所以，，

因为，

所以，

所以.

设每台发动机获得的奖励为（万元），则的分布列为：

	0	2	5
	0.0228	0.8185	0.1587

所以每台发动机获得奖励的数学期望为

（万元）.