
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为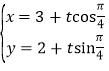 (其中
(其中![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
科目:高中数学 来源: 题型:
【题目】鲤鱼是中国五千年文化传承的载体之一,它既是拼搏进取、敢于突破自我、敢于冒险奋进精神的载体,又是富裕、吉庆、幸运的美好象征.某水产养殖研究所为发扬传统文化,准备进行“中国红鯉”和“中华彩鲤”杂交育种实验.研究所对200尾中国红鲤和160尾中华彩鲤幼苗进行2个月培育后,将根据体长分别选择生长快的10尾中国红鲤和8尾中华彩鲤作为种鱼进一步培育.为了解培育2个月后全体幼鱼的体长情况,按照品种进行分层抽样,其中共抽取40尾中国红鲤的体长数据(单位:![]() )如下:
)如下:
5 | 6 | 7 | 7.5 | 8 | 8.4 | 4 | 3.5 | 4.5 | 4.3 |
5 | 4 | 3 | 2.5 | 4 | 1.6 | 6 | 6.5 | 5.5 | 5.7 |
3.1 | 5.2 | 4.4 | 5 | 6.4 | 3.5 | 7 | 4 | 3 | 3.4 |
6.9 | 4.8 | 5.6 | 5 | 5.6 | 6.5 | 3 | 6 | 7 | 6.6 |
(1)根据以上样本数据推断,若某尾中国红鲤的体长为![]() ,它能否被选为种鱼?说明理由;
,它能否被选为种鱼?说明理由;
(2)通过计算得到中国红鲤样本数据平均值为![]() ,中华彩鲤样本数据平均值为
,中华彩鲤样本数据平均值为![]() ,求所有样本数据的平均值;
,求所有样本数据的平均值;
(3)如果将8尾中华彩鲤种鱼随机两两组合,求体长最长的2尾组合到一起的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)试问:在![]() 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点![]() ,使得
,使得![]() 的外心在
的外心在![]() 上?若存在,求
上?若存在,求![]() 的坐标;若不存在,请说明理由..
的坐标;若不存在,请说明理由..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”(已知1丈为10尺)该锲体的三视图如图所示,则该锲体的体积为( )
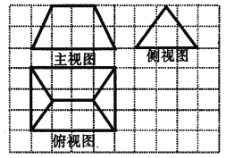
A. 12000立方尺B. 11000立方尺
C. 10000立方尺D. 9000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到其准线的距离为
的焦点到其准线的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,问抛物线
两点,问抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是正三角形?若存在,求出点
是正三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
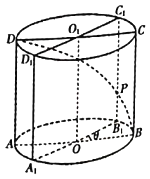
【题目】如图,已知圆柱![]() ,底面半径为1,高为2,
,底面半径为1,高为2,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其路径最短时在侧面留下的曲线记为
,其路径最短时在侧面留下的曲线记为![]() :将轴截面
:将轴截面![]() 绕着轴
绕着轴![]() ,逆时针旋转
,逆时针旋转![]()
![]() 角到
角到![]() 位置,边
位置,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
(1)当![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() ;
;
(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com