
分析 先通过分类讨论求出f[f(x)]的表达式(分四段),再运用数形结合的方法得出两图象有三个交点.
解答  解:∵x∈[0,1],根据题意,令|2x-1|≥$\frac{1}{2}$,
解:∵x∈[0,1],根据题意,令|2x-1|≥$\frac{1}{2}$,
解得x∈[0,$\frac{1}{4}$]∪[$\frac{3}{4}$,1],所以,
①当x∈[0,$\frac{1}{4}$]时,f(x)=1-2x,
f[f(x)]=2(1-2x)-1=-4x+1;
②当x∈[$\frac{3}{4}$,1]时,f(x)=2x-1,
f[f(x)]=2(2x-1)-1=4x-3;
同理,令|2x-1|<$\frac{1}{2}$,解得x∈($\frac{1}{4}$,$\frac{3}{4}$),得到,
③当x∈($\frac{1}{4}$,$\frac{1}{2}$]时,f(x)=1-2x,f[f(x)]=1-2(1-2x)=4x-1;
④当x∈($\frac{1}{2}$,$\frac{3}{4}$)时,f(x)=2x-1,f[f(x)]=1-2(2x-1)=-4x+3.
所以,x∈[0,1]时,记y=h(x)=f[f(x)]=$\left\{\begin{array}{l}{-4x+1,x∈[0,\frac{1}{4}]}\\{4x-1,x∈(\frac{1}{4},\frac{1}{2}]}\\{-4x+3,x∈(\frac{1}{2},\frac{3}{4}]}\\{4x-3,x∈(\frac{3}{4},1]}\end{array}\right.$,
画出函数y=h(x)(紫线)和y=-lnx(蓝线)的图象,如右图:
显然,两函数图象有三个交点(可以考察x=$\frac{1}{2}$处的函数值来判别交点个数),
所以,原函数g(x)=f(f(x))+lnx在[0,1]上有3个零点,
故答案为:3.
点评 本题主要考查了根的存在和个数的判断,涉及分段解析式的确定,体现了分类讨论,数形结合的解题思想,属于难题.


科目:高中数学 来源: 题型:选择题
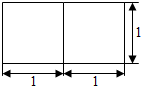
| A. | $\frac{16}{3}$ π | B. | $\frac{19}{3}$ π | C. | $\frac{19}{12}$ π | D. | $\frac{4}{3}$ π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
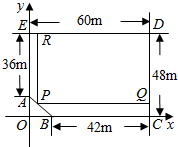 某房地产公司要在荒地ABCDE上划出一块矩形地面DRPQ建造一幢公寓.
某房地产公司要在荒地ABCDE上划出一块矩形地面DRPQ建造一幢公寓.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1 | B. | 3:1 | C. | 9:1 | D. | 1:9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
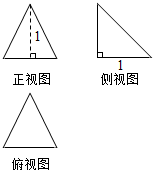
| A. | $\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$ | B. | $\frac{{\sqrt{6}+2}}{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$ | D. | $\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com