
| A. | $\frac{16}{3}$ π | B. | $\frac{19}{3}$ π | C. | $\frac{19}{12}$ π | D. | $\frac{4}{3}$ π |
分析 由已知得该三棱柱的底面棱长为2,高为1的正三棱柱,先求出底面外接圆半径和球心到底面的球心距,从而能求出球半径,由此能求出该球的表面积.
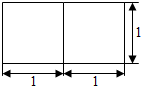
解答 解:由已知底面是正三角形的三棱柱的正视图
我们可得该三棱柱的底面棱长为2,高为1
则底面外接圆半径r=$\frac{2\sqrt{3}}{3}$,球心到底面的球心距d=$\frac{1}{2}$,
则球半径R2=$\frac{4}{3}+\frac{1}{4}$=$\frac{19}{12}$,
则该球的表面积S=4πR2=$\frac{19}{3}π$.
故选:B.
点评 本题考查三棱柱的外接球的表面积的求法,是中档题,解题时要认真审题,注意正三棱柱的结构特征和球的性质的合理运用.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
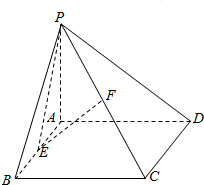 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
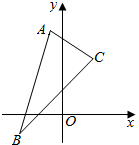 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com