
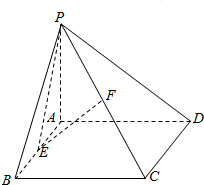
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点 分析 (1)证明PA⊥BC,AB⊥BC,证得CB⊥平面PAB,从而有CB⊥PE.
(2)取CD的中点G,由FG是三角形CPD的中位线,可得 FG∥PD,再由举行的性质得 EG∥AD,证明平面EFG∥平面PAD,从而证得EF∥平面PAD.
解答 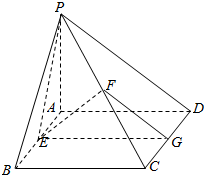 解:(1)证明:∵侧棱PA垂直于底面,∴PA⊥BC.
解:(1)证明:∵侧棱PA垂直于底面,∴PA⊥BC.
又底面ABCD是矩形,∴AB⊥BC,
这样,CD垂直于平面PAD内的两条相交直线,∴CB⊥平面PAB,
∴CB⊥PE.
(2)取CD的中点G,
∵E、F分别是AB、PC的中点,∴FG是三角形CPD的中位线,
∴FG∥PD,FG∥面PAD.∵底面ABCD是矩形,∴EG∥AD,EG∥平面PAD.
故平面EFG∥平面PAD,∴EF∥平面PAD.
点评 本题考查证明线线垂直、线面平行的方法,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:选择题
若新高考方案正式实施,甲,乙两名同学要从政治,历史,物理,化学四门功课中分别选取两门功课学习,则他们选择的两门功课都不相同的概率为( )
A.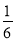 B.
B. C.
C.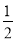 D.
D.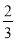
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,3} | C. | {0,2,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
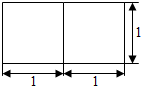
| A. | $\frac{16}{3}$ π | B. | $\frac{19}{3}$ π | C. | $\frac{19}{12}$ π | D. | $\frac{4}{3}$ π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com