
分析 由已知可得x2-2x-8≥(m+2)x-m-15,x>2恒成立,即m≤$\frac{{x}^{2}-4x+7}{x-1}$=(x-1)+$\frac{4}{x-1}$-2,x>2恒成立,结合基本不等式求出m的范围,可得实数m的最大值.
解答 解:∵f(x)=x2-2x-8,
若对一切x>2均有f(x)≥(m+2)x-m-15成立.
则x2-2x-8≥(m+2)x-m-15,x>2恒成立,
即m≤$\frac{{x}^{2}-4x+7}{x-1}$=(x-1)+$\frac{4}{x-1}$-2,x>2恒成立,
∵x-1>1,
故(x-1)+$\frac{4}{x-1}$-2≥2$\sqrt{(x-1)\frac{4}{x-1}}$-2=2,
当且仅当x=3时,(x-1)+$\frac{4}{x-1}$-2取最小值2,
故m≤2,
即实数m的取值最大为2,
故答案为:2.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
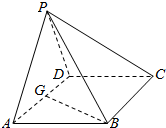 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABD,G为AD的中点,则点G到平面PAB的距离为( )
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABD,G为AD的中点,则点G到平面PAB的距离为( )| A. | $\frac{{\sqrt{15}}}{10}a$ | B. | $\sqrt{5}a$ | C. | $\frac{{\sqrt{5}}}{5}a$ | D. | $\sqrt{15}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (1,3) | C. | (2,3) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
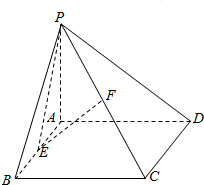 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个点与一条直线 | B. | 两个点或一条直线或一个圆 | ||
| C. | 两个点 | D. | 两条射线和一个圆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com