
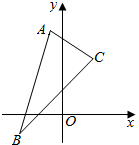
 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).分析 利用直线的两点式方程、点斜式方程、直线 的斜率公式和点到直线的距离公式求解
解答 解:(1)∵B(-2,-1),C(2,3),
∴BC的中点D(0,1),又A(-1,4),
∴直线AD:$\frac{y-1}{4-1}=\frac{x}{-1}$,整理,得:3x+y-1=0.…(4分)
(2)∵△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3),
∴AC的中点E($\frac{1}{2}$,$\frac{7}{2}$),AC的斜率k=-$\frac{1}{3}$,
∴AC边上的垂直平分线的斜率为3,
∴所求直线方程y-$\frac{7}{2}$=3(x-$\frac{1}{2}$),整理,得:3x-y+2=0 …(8分)
(3)∵B(-2,-1),C(2,3),
∴直线BC:$\frac{y+1}{3+1}=\frac{x+2}{2+2}$,整理,得:x-y+1=0,
∴BC边上的高的长即点A(-1,4)到直线BC的距离,其值为d=$\frac{|-1-4+1|}{\sqrt{{1}^{2}+(-1)^{2}}}$=2$\sqrt{2}$.
点评 本题考查直线方程的求法,考查线段长的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
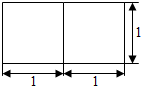
| A. | $\frac{16}{3}$ π | B. | $\frac{19}{3}$ π | C. | $\frac{19}{12}$ π | D. | $\frac{4}{3}$ π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0] | B. | [-3,0) | C. | [-3,0)∪{2} | D. | [-3,0]∪{2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
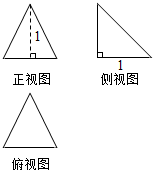
| A. | $\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$ | B. | $\frac{{\sqrt{6}+2}}{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$ | D. | $\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com