Question

19．已知函数f（x）=e^x+alnx的定义域是D，关于函数f（x）给出下列命题：
①对于任意a∈（0，+∞），函数f（x）是D上的增函数
②对于任意a∈（-∞，0），函数f（x）存在最小值
③存在a∈（0，+∞），使得对于任意的x∈D，都有f（x）＞0成立
④存在a∈（-∞，0），使得函数f（x）有两个零点
其中正确命题的序号是①②④．

Answer 1

分析 ①由a∈（0，+∞）时，f′（x）=e^x+$\frac{a}{x}$≥0说明①正确；由函数在定义域内有唯一的极小值判断②正确；画图说明③错误；结合②的判断可知④正确．

解答 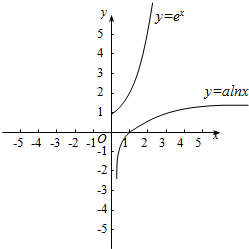解：函数的定义域为：（0，+∞），f′（x）=e^x+$\frac{a}{x}$．
①∵a∈（0，+∞）∴f′（x）=e^x+$\frac{a}{x}$≥0，是增函数．∴①正确；
②∵a∈（-∞，0），∴f′（x）=e^x+$\frac{a}{x}$=0有根x₀，且f（x）在（0，x₀）上为减函数，在（x₀，+∞）上为增函数，∴函数有极小值也是最小值，②正确；
③画出函数y=e^x，y=alnx的图象，由图可知③不正确；
④由②知，a∈（-∞，0）时，函数f（x）存在最小值，且存在a使最小值小于0，且当x在定义域内无限趋于0和趋于+∞时f（x）＞0，可知存在a∈（-∞，0），f（x）=e^x+alnx=0有两个根，④正确．
故答案为：①②④．

点评 本题考查命题的真假判断与运用，考查了利用导数研究函数的单调性，最值等问题，属中档题．